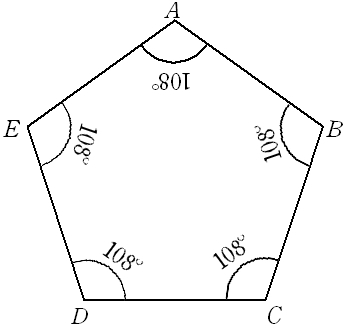
正多角形を作図して複数のグラフにプロットしてみます。 メニューを開く 正三角形、正四角形、正五角形とかをグラフで描くだけ?あんまり面白そうじゃないね。 グラフの作図練習になるからやってみよう。 ラジャー。正多角形はどうやってグラフで描くの? 角度をもとに円周上の頂点正十五角形 正十五角形においては、中心角と外角は24 °で、内角は156°となる。 一辺の長さが a の正十五角形の面積Sは = = ( ) (/) は有理数と平方根の組み合わせのみで表せる = = ( ) 正十五角形の作図 正十五角形は古代から定規とコンパスによる作図が可能であることが知られていた図形第314問 正五角形と角度 図形ドリル 5年生 6年生 new 正五角形 角度 ★★★☆☆☆ (中学入試標準レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げてい

数学の角度の問題 下の図のように 1辺の長さが等しい正五角形と正六 数学 教えて Goo
正五角形 角度
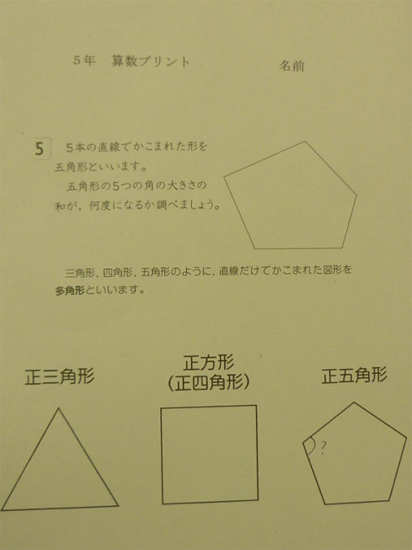
正五角形 角度-2 然后正面对着镜子观察自己的脸型,脸的长度(1),额头最宽处(2),颧骨最宽处(3),下巴最宽处(4),用皮尺分别测量出来,记下。 3 最后进行简单的对比,就可以大致确定了自己的脸型了。 那么你的脸型更接近哪一款呢? 鹅蛋脸 鹅蛋形脸被 正方形と同じように、頂点dから対角線を2本引きます。すると三角形が3つあることが分かります。なので、正五角形は「 三角形の内角「180度」×3個分 = 540度 」になります。また、正五角形は、同じ角度の角が5つなので、「 540度 ÷ 5つ = 108度 」です
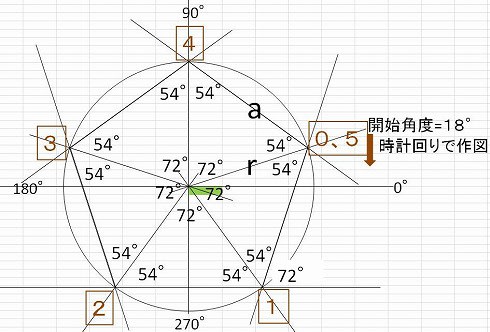



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみました 日だまりのエクセルと蝉しぐれ
正五角形の回転角度を変えると星になる 正五角形が描けると、星を描くのは実は簡単です。 回転する角度を変えればいいだけです。 論より証拠でやってみます。 まずは、72度 → 144度(72度×2)にしてみます。 こうすると、以下のような星が描けます。 さらに角度を変更してみます。正五角星可分割成5个3角形和1个正五边形 五个3角形各自角度之和180 正五边形的内角和180*(n2)=180*3=540;每个角时540/5=108 三角形的是等腰三角形,底角是五边形的外角,即底角==72 三角形内角和为180,那么三角形顶角,即五角星尖角=*2=36 已赞过 已踩过 你对这个回答的评价是? 评论 收起 下の図のような星型の図形があります。星の中にある五角形は正五角形です。このときの①の角度は何度になるか求めなさい。 解説 まず初めに、正五角形の1つの内角の大きさを求めます。正五角形の内角の和は、 180°×(52)=540° 正五角形なので一つひとつの内角は等しいでの、 540÷5=108° 360
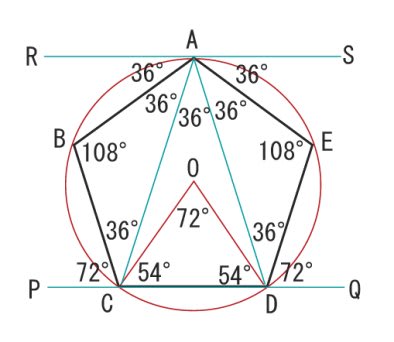
正五邊形不能鑲嵌平面,因為其內角是108°,不能整除360°。截至15年 (!) ,17年5月,里昂高等师范学校Michaël Rao宣称已证明只存在15种凸五边形鑲嵌平面情况。 。 面積公式推導 正多邊形的面積公今回は、角度だけに絞って この正五角形を見てみますと このようになります。 ここで rs//pq です。 ocdの底角を計算するときも、 この ocdをタテ半分に分けて、直角三角形を作り 90-36 で、54° これなら 暗算でできそうですね。 このように 36°と54° 、そしてそれらの2倍の72°と108 正五角形の内角の大きさは「108°」ってことさ。 くそ便利でしょ??^_^ なぜ正多角形の内角が計算できるの?? でもでも、なんで、 180× (n2)/n で計算できちゃうんだろう?? 都合よすぎるよね?笑 なぜそうなるの?? ってことを確認してみよう。 正多角形の内角の和っていく
立方体の切断面が正五角形にならないのはなぜですか? 参考書には正五角形の一つの角は108度だが、この場合は90度以上になれない角があるからと書いてありましたが、よくわかりません。 補足 平行を使う見分け方は理解できましたが、角度を使った 株式会社ベネッセコーポレーションのプログラミング教育の取り組みや、プログラミング教育に関する国内外のニュースや事例を紹介するWebページです。 小5算数 内角の大きさを求めて正多角形を作図しよう について紹介します。 正五角形の一辺の長さ 先ほどの図に点の名前をかき加えて考えてみます。時計回りに a から e と名前を付けます。 点 o は好きな場所で、半径も好きな長さでした。 点 a の場所は円周上の点であればどこでもいいです。 これらを決めれば、 b から e が決まります。 。この4点をどのように



角度 五角形 中学から数学だいすき




発展 円に内接する正五角形の作図 デザインあ おとなスペシャルで紹介されてたやつ なかけんの数学ノート
そして、あなたは正五角形を持っています: 下のマークから折りたたみ、右のマークを上の線に合わせることは、構造に必要な角度を作成することによって、最も重要な部分のようです。 この折り目は私に 折り紙の三等分を思い出させます。 これは近似 >五角形の頂点で向けるべき角度を求められれば、書くべきコードが分かると思います。 ご提案いただきありがとうございます。 キャンセル 完了する link 2 正方形のソースで既にされてますが、正多角形は180(多角形の内角)を多角形の角の数だけ書けばできます。 そして正多角形の内タヌキ 正5角形の内角の和を計算すると 5角形は三角形3つに分けることができるから 180×3=540°となります。 キツネ 正5角形は5つの等しい内角でできていて この5つの角度の和は、540°だから、 1つの角は 540÷5=108°と計算できます。 五角形の外角




角xの求め方を教えて下さい 答えは17度です Clearnote



早稲田11 2 の 1 角度 正五角形と正三角形が重なった図形 気まぐれ解説カフェ 仮
数学科目 将五角星看作是5个重叠在一起的三角形 即五个三角形的和为5乘以180°为900° 再减去五角星中间的那个五角形的 正五角形の性質 正三角形・正方形・正六角形に引き続き、正五角形編です。 相似 まずは角度に注目。 内角の和が540°なので、1つの内角が 108° 。 対角線を引いたら内角が 3等分 されます。 分解してできる三角形の内角は、 36°、72°、108°の3種類 。 そして、 36°72°108°=123 になっ 今回は正五角形に隠された秘密を解き明かしてみましょう。 角度 まずは、角度。 対角線を引いた正五角形の中に現れる角度は何種類でしょうか? 最初に、正五角形の内角の和を求めます。正五角形は3個の三角形に分割されるので、内角の和は180°×3=540




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか




ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみました 日だまりのエクセルと蝉しぐれ
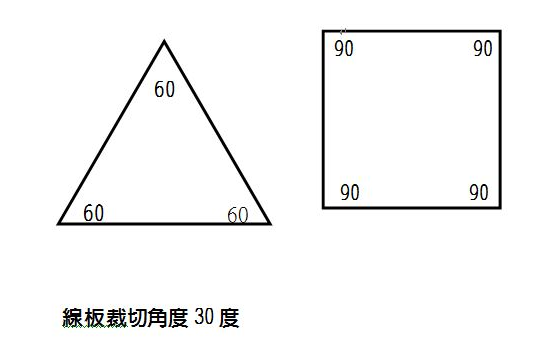
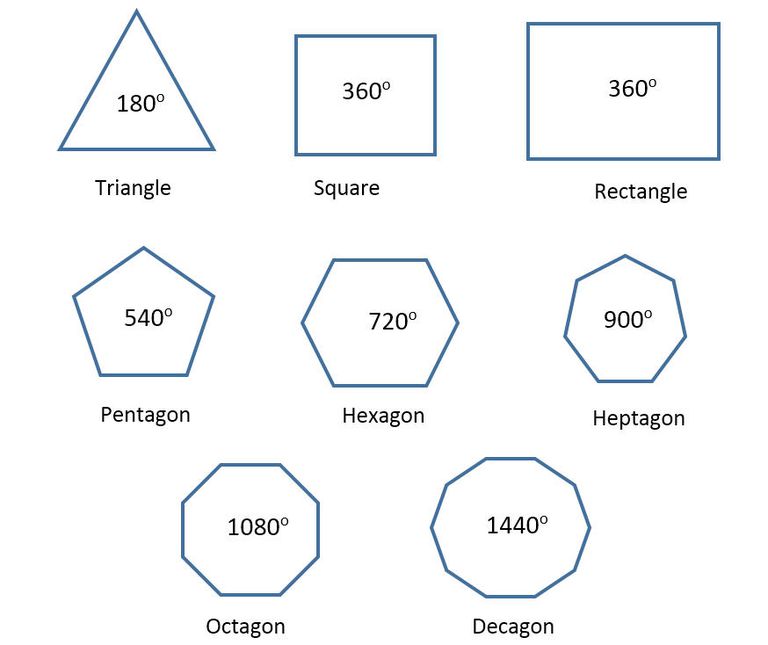
正五角形の1つ分の外角は72°となるので 内角1つ分の大きさは $$\large{=108°}$$ となります。 同様に 正六角形の1つ分の内角は\(=1°\) 正八角形の1つ分の内角は\(=135°\) 正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の 三角形の角度の合計は180度です 🔊 Play The angles of an equilateral triangle are all 60 degrees 正三角形の角度は、すべて60度です 🔊 Play The area of triangles is half of the base times the height 三角形の面積は、底辺×高さ÷2です 四角形 quadrangle, quadrilateral



角度 五角形 中学から数学だいすき




数学の角度の問題 下の図のように 1辺の長さが等しい正五角形と正六 数学 教えて Goo
看板の平米数の算出。自分で出した正五角形の面積が正確かどうか確かめたかった。 合ってて良かった。 8 0025 30歳代 / 会社員・公務員 / 役に立った / 使用目的 建築物の面積・体積の計算 9 0141 歳代 / 会社員・公務員 / 役に立った / 使用目的 養殖用生け簀の面積の算円内接の正五角形を書きたかったが、分度器なし、コンパスなし・・・ ご意見・ご感想 最初にある円が不完全だったのか、数ミリ誤差が生まれた。 2 0533 60歳以上 / 教師・研究員 / 役に立った / 使用目的 万華鏡の筒に内接する正多角形の一辺を計算で求めたかった。しかし、角数が問題 (奈良学園登美ヶ丘中学 09年、早稲田中学 10年 女子学院中学 14年 受験問題 算数) 難易度★★★ 1 1辺の長さが等しい正五角形と正六角形を、下の図Ⅰのように1つの辺を重ねました。このとき、アの角度は何度ですか。



正五角形です あ い うの角度の求め方教えてください あ36 Yahoo 知恵袋



上6 角形五角形角度 シモネタ
小学5年生 小学校算数 多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月正三角形の角度問題 まとめ お疲れ様でした! 正三角形の性質としては このように単純な性質しかないので 問題としては、いろんな図形との融合で出題されがちです。 正三角形どうしの融合の場合 60°の角になるところをしっかりと見つけていくこと さっきの三角形、正五角形の中にできてる三角形のそれぞれの角度が分かれば、答えが出せるんじゃねぇーか? ミズキ 察しがいいね、カイちゃん。そうやって推測することは大切だね。 ミズキ それじゃ、正五角形の中にある二等辺三角形のそれぞれの底角はいくつになるかな? カイト 底角



正多边形形状十字形角度 圆形png剪贴画白色 单色 多边形 黑色 单免抠素材下载 图片id 其它元素 Png素材 素材宝scbao Com




如何求正多边形的面积 Find The Area Of Regular Polygons Tl80互动问答网
長さの比、角の二等分線の定理 (浅野中学 13年) ;回答 (2件中の1件目) 作図で重心を見つける方法の質問だと解釈し、説明します。正五角形の対角線は下図の青線のようになり、これだけでは重心が見つかりません。下図の対角線 {\rm BD} と {\rm CE} の交点を {\rm A}'、同様に、{\rm B}', {\rm C}', {\rm D}', {\rm E}' を定めていきます。 1つの頂点に正五角形が3枚ずつ集まると正十二面体ができますが、正五角形の1つの内角は108度なので、正五角形4枚の角度の和は360度以上となり、これ以上の枚数の正五角形で正多面体を作ることはできません。 これが、正多面体が5種類しかない理由です。 (数学科 園田) "Only 5 kinds of Regular



1



五角星与等腰三角形 1 4角平分线的性质 初中湘教版13版 数学中国网
正五角形の性質(三角形の相似、黄金比、等脚台形、ひし形) スポンサーリンク 高校数学A 平面図形 検索用コード 角度 dy} {l} 対角線を引いてできるすべての角度は$ {36°,\ 72°,\ 108°$のいずれかである} 対角線 {AC,\ AD}を引くと正五角形は3個の



Lとmは平行であり 五角形abcdeは正五角形である Xの Yahoo 知恵袋
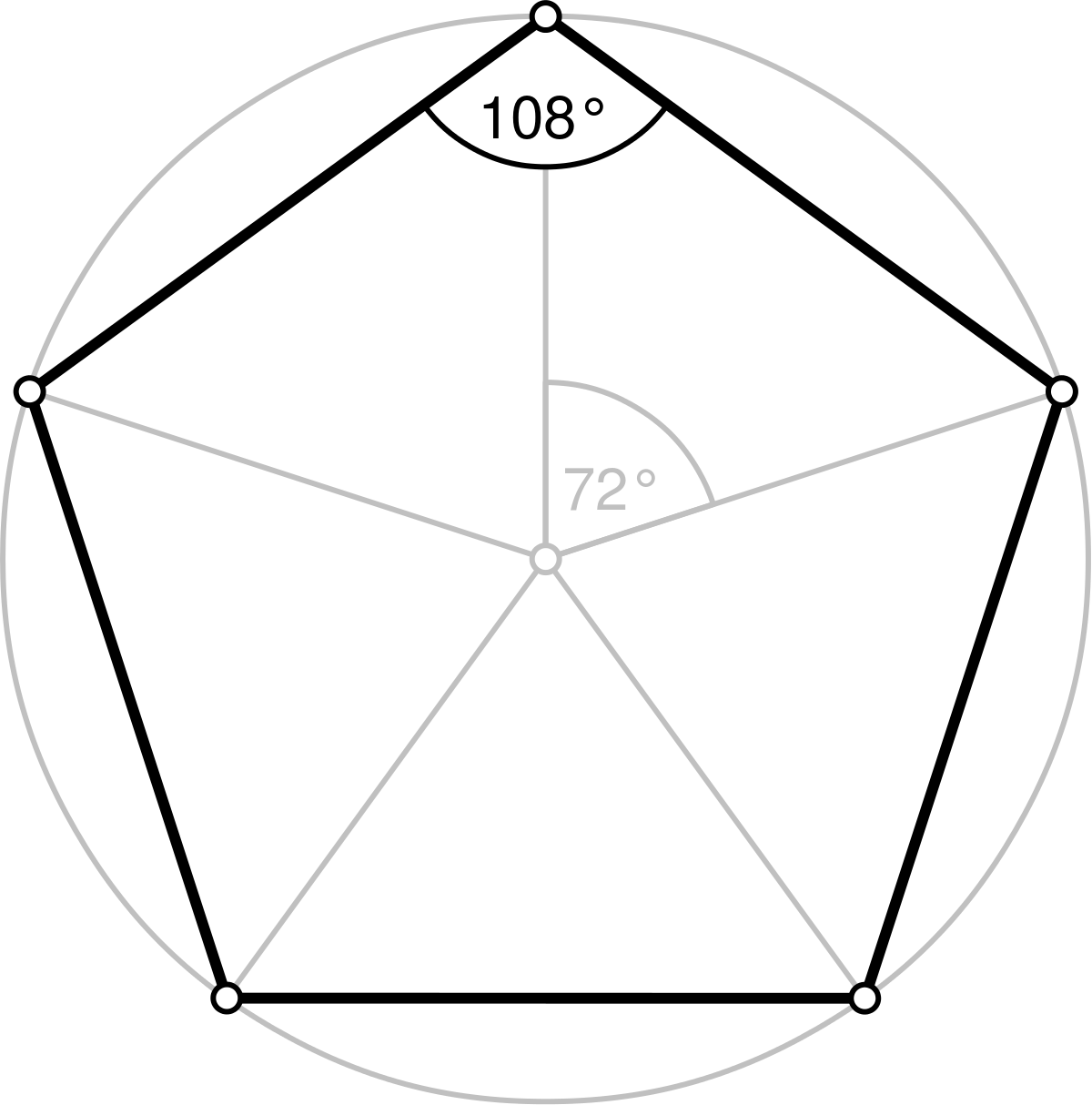



五边形 维基百科 自由的百科全书




多边形的内角



1



六边形 维基百科 自由的百科全书




凹五边形第1页 驾考预约大全




如何计算角度 8 步骤 包含图片



重なった正六角形と正五角形の角度 奈良学園登美ヶ丘中学 09年 早稲田中学 10年 算数解法の極意




孙嘉怡 0ec8fd6fbcf0e3f7b515a50c7d7ee6 个人资料 Pinterest
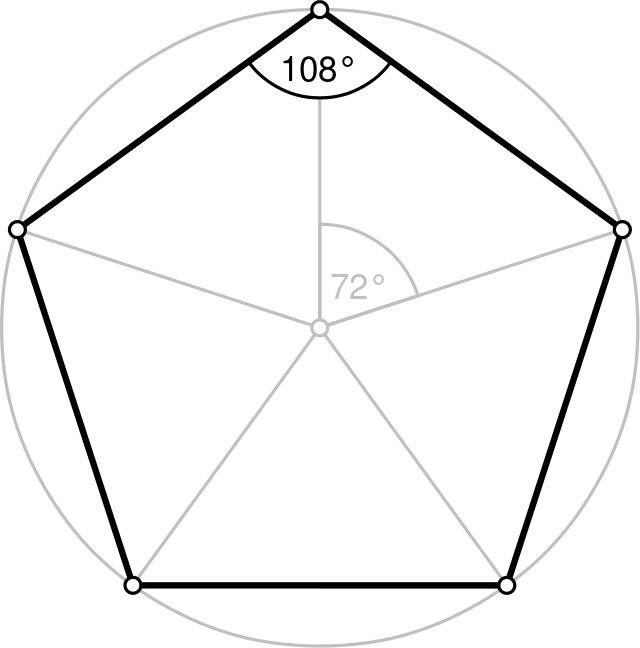



五边形 维基百科 自由的百科全书




Javascript怎么画正五边形 Html中文网




六角形角度 六角形和八角形的角度分別是多少 作業幫 Enhti



茗渓予備校 科目情報
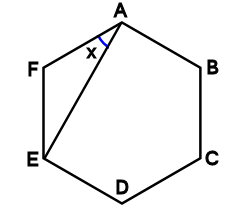



上6 角形五角形角度 シモネタ




如何求正多边形的面积 Find The Area Of Regular Polygons Tl80互动问答网




六角形五角形英文六角形的中的英文 中文 英文字典 格洛斯貝 Doreff




正五角形というだけで 分かる角度は 名寄 算数数学教室より 数学教室 算数 数学




十角形 十角形 Zhz Wiki



折った正五角形の角度 ラ サール中学 2014年 これが中学入試に出た図形問題



五边形 Wikiwand




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか




五角星内角和怎么算 五角星的内角和为几度 如何证明 三人行教育网 Www 3rxing Org



図形 正五角形の分解 父ちゃんが教えたるっ



数学得意な方お願いします 正五角形の1つの内角は何度になりますか その角度を求 Yahoo 知恵袋




正五角星每个锐角度数正五角星的每一个锐角的度数



図 正五角形abcdeは正五角形で 三角形fcdは正三角形です xの角度を求め Yahoo 知恵袋




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す




小学校5年 算数 正多角形の角の大きさ Youtube



古老正五邊形畫法 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌
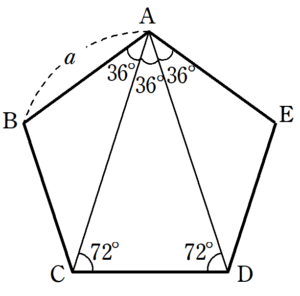



正多角形の面積の公式 Fukusukeの数学めも



六角形五角形英文六角形的中的英文 中文 英文字典 格洛斯貝 Doreff



上6 角形五角形角度 シモネタ
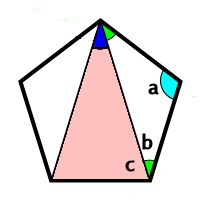



正五角形の中の角度
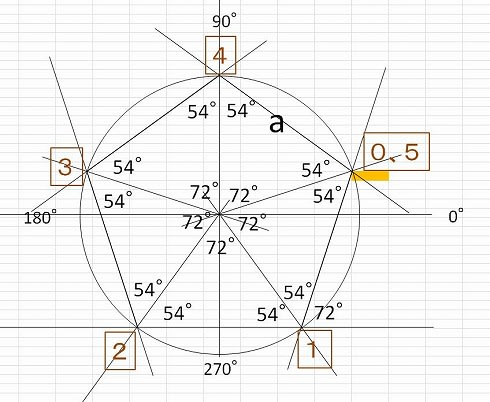



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみましたpart 2 日だまりのエクセルと蝉しぐれ
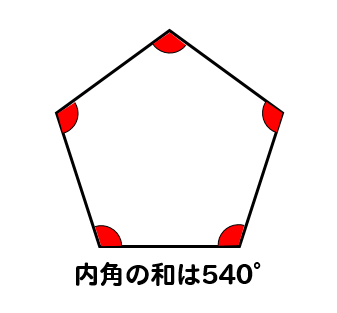



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




3种方法来求五边形的面积



少し傾いた正五角形に二本の平行線を引いた場合のxとyの角度の Yahoo 知恵袋



平面図形の角度 第81問 正五角形 女子学院中学 入試問題 13年 平成25年度 算数 まいにち一題 中学受験過去問題研究




File Dodeca0 Jpg Wikimedia Commons
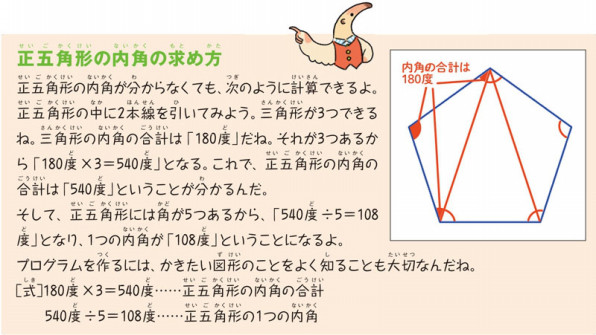



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




正多边形 属性



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス



正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp



問題 數學習題幫忙 場外休憩區哈啦板 巴哈姆特




どこで間違えてるか教えて下さい ˊᵕˋ Xの角度を求める問題です Clearnote



正五角形
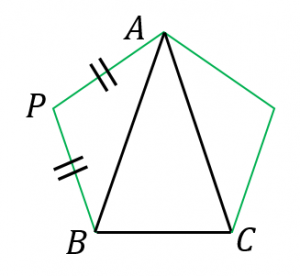



正五角形の対角線の長さと高さ 具体例で学ぶ数学



五边形 Wikiwand




國中生常考的正五邊形角度問題 Youtube
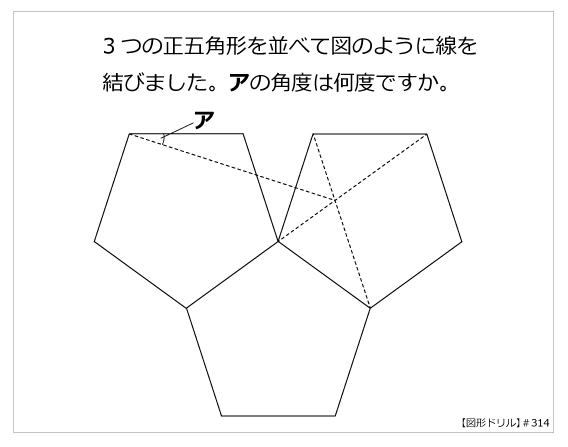



第314問 正五角形と角度 図形ドリル 第314問 正五角形と角度 算数星人のweb問題集 中学受験算数の問題に挑戦
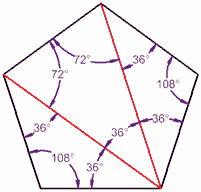



多边形的内角




球面三角法 Cn Wikitonghop Com



早稲田11 2 の 1 角度 正五角形と正三角形が重なった図形 気まぐれ解説カフェ 仮



五角形面積五角形的面積 Lousi Imagine



等边五边形 万图壁纸网
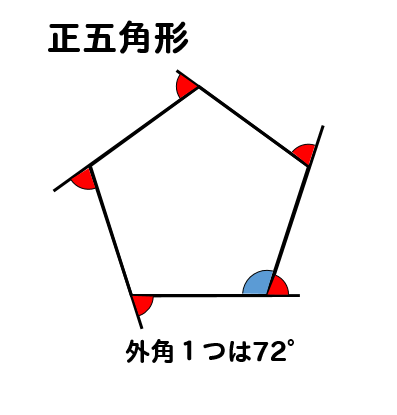



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




正多边形形状十字形角度 圆形png剪贴画白色 单色 多边形 黑色 单免抠素材下载 图片id 其它元素 Png素材 素材宝scbao Com




自然の幾何学 正五角形 セイヨウキョウチクトウ Piziadasgraficas



1




正五角星每个锐角度数正五角星的每一个锐角的度数



上6 角形五角形角度 シモネタ




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




正五边形计算器



高雄宅速修室內裝修企業有限公司 高雄水電維修工程




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか




多边形的内角
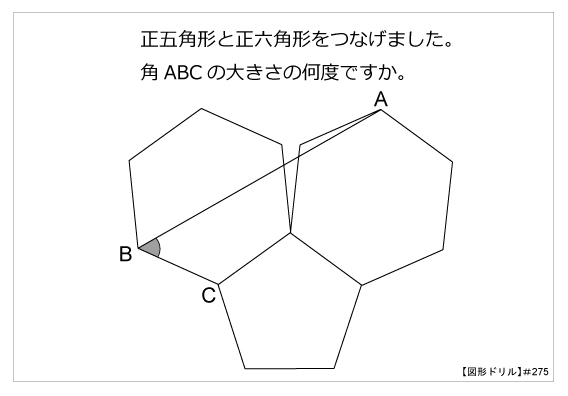



第275問 正五角形と正六角形 図形ドリル 第275問 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦




圓內接多邊形 维基百科 自由的百科全书



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス



1




中学受験算数 女子学院中学校 17年 正五角形の中に書かれた正三角形で作られた角度を求める問題 Youtube



正五角形



平面図形の角度 第34問 女子学院中学 10年 平成22年度 受験問題 算数 まいにち一題 中学受験過去問題研究




Katsunou Brain Teaser Mind Jewel Puzzle




正多邊形圖學 數位典藏與學習聯合目錄



多邊形幾何 五角形 六邊形和十二邊形
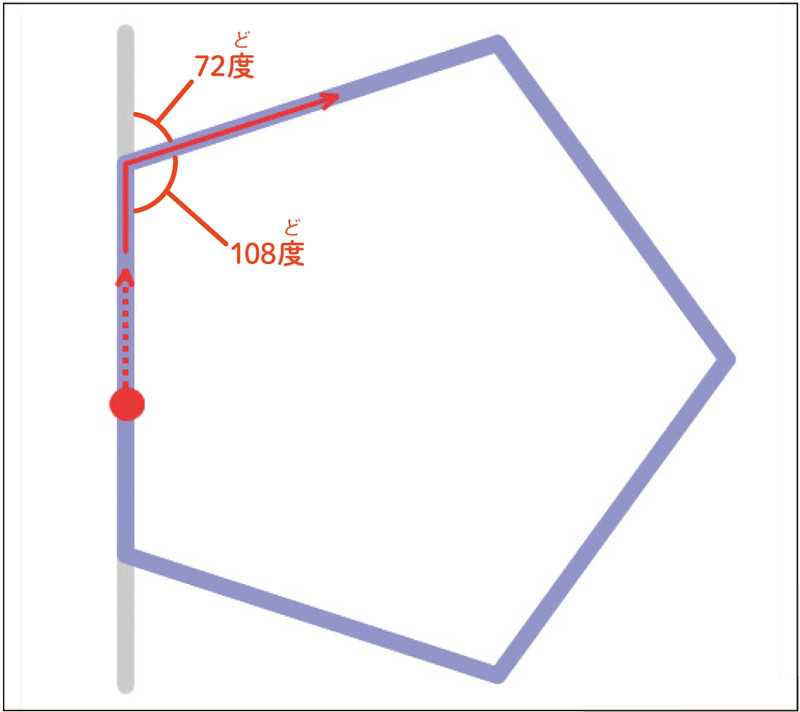



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




正方形に内接する面積最大の正五角形 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



五边形简笔画图案大全 万图壁纸网




五角星的内角和怎么求 五角星的内角和是多少 三人行教育网 Www 3rxing Org
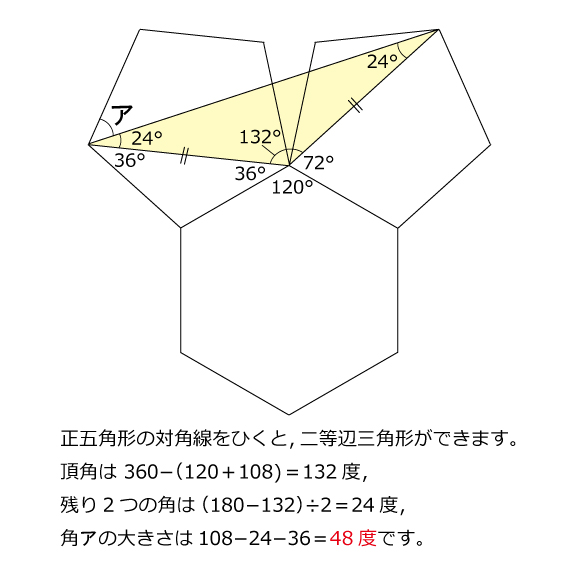



早稲田中 正五角形と正六角形21年早稲田中 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦
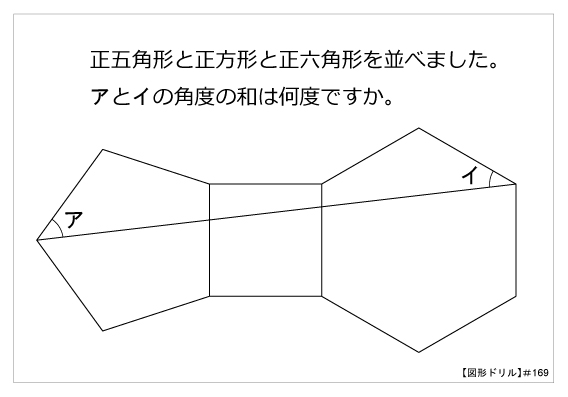



上6 角形五角形角度 シモネタ




如何计算角度 8 步骤 包含图片



正五边形尺规作图 快懂百科
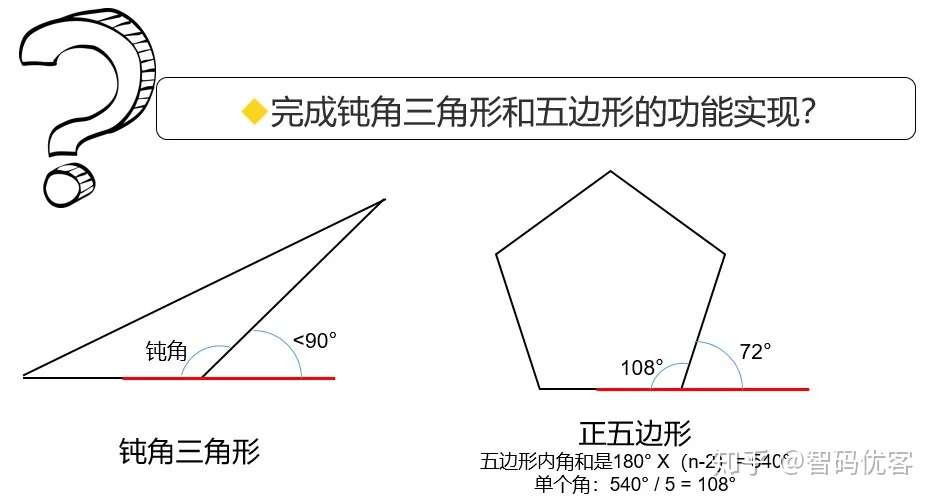



Scratch Ai 数学 美丽的几何图案第4节 共4节 知乎




上6 角形五角形角度 シモネタ



上6 角形五角形角度 シモネタ



Xの角度を教えてください円の中は正五角形です 正五角形の各頂 Yahoo 知恵袋




如何利用编程机器人程小奔编程玩几何 Makeblock




五边形 Wikiwand



0 件のコメント:
コメントを投稿