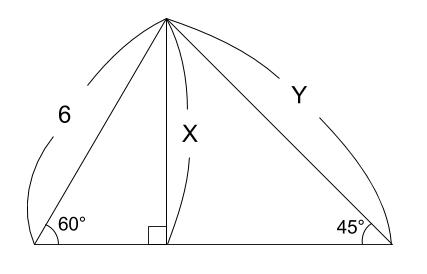
ADの長さをx, DCの長さをyとする。 ABDで三平方の定理を使うと 9 2 = (10−y) 2 x 2 ・・・① ADCで三平方の定理を使うと 11 2 =x 2 y 2 ・・・② ②を変形してx 2 =11 2 −y 2 これを①に代入すると 9 2 = (10−y) 2 11 2 −y 2 81=100−yy 2 121−y 2 y=−8117/6/ 高校講座HOME >> ベーシック数学 ベーシック数学 Eテレ 毎週 月曜日 午後2:00〜2:10 ※この番組は、前年度の再放送です。 出演者紹介 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に
受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学
三平方の定理 比 計算
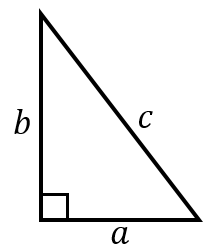
三平方の定理 比 計算-三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。三平方の定理による辺の長さの計算です。 三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
三平方の定理の拡張(中学校の数学との関係) 右図1のような直角三角形については、 a 2 =b 2 c 2 (1) が成り立ちます。(三平方の定理) では、図2のように∠ A が 90 ° でないときには、この定理はどんな形になるのでしょうか。直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。直角二等辺三角形の底辺と高さの長さは同じです。底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11三角比 三平方の定理 直角三角形・三平方の定理 三平方の定理 c a b C A B 直角三角形においては a2 b2 = c2 ∠C = 90 となったとき余弦定理で cosC = 0 としたもの。 極めて重要な
16/6/19 三平方の定理 225°,\ 675°の三角比は数II}で半角の公式を学習すると割と容易に求められる よって,\ 15°,\ 75°の三角比と同じく参考程度の問題である まず,\ 各辺の長さをすべて求める\ 本問の2重根号ははずせない このため,\ 有理化を含めた式変形が厄介About this project 本サイトは、全国約12万6千人(16年時点) の不登校などで個別指導を必要とする子どもたちや、全国約3万4千人(16年時点) の日本語指導を必要とする外国人の子どもたちのために、 多言語に対応した数学学習コンテンツです。 いつでも、どこでも、どの段階からでも、 3分間解答 左の直角三角形は、正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 よって、下の図のように長さが決まります。 x= 3√3 x = 3 3 です。 右の直角三角形は、正方形を半分にした直角二等辺三角形です。 3 3 辺の比は暗記で、 11√2 1 1 2 です。 よって、下の図のように長さが決まります。 y= 3√6 y = 3 6 です。
・相似な図形の性質や比の計算方法を 確認させる。 三平方の定理を平面図形に応用するため には、その図形の中に直角三角形を見つけ る。直角三角形が見えないときは、補助線を 引き直角三角形を作る。 特別な直角三角形では、3辺の長さの間4/3/19 まぁ、三平方の定理でも解けますね。 しかし、もし、4ではなく04などの小数や分数が出た場合は、ちょっと計算が苦しくなります。 あくまでも、一時しのぎと考えて使ってください。 本来は、 比を利用するのがベスト です。 Tweet ← 受験数学:三平方31/5/16 これを「三平方の定理」といいます。 こんな問題が出ます。 問題 こんな問題、皆さんならどうやって解きますか? えーと・・・c 2 =b 2 a 2 だから、 25の二乗= b 2 7の二乗だから・・・ 25の二乗=625 7の二乗=49 625= b 2 49 ここから移項して b 2 =625-49 b 2 =576



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
三平方の定理とは、 「不思議な直角三角形」の不思議さを説明したもの です。 直角三角形は、上の図のような形をしていて、内側の 3 つの角のうち、 1 つが 90 度になっています。 90度(直角)を挟む辺の長さを b 、 c として、斜辺を a とすると、次の関係が成り立ちます。 a 2 =b 2 c 2 a 2 は「 a の二乗」といい、「 a × a = a2 」と表記します。 a 2 =b 2 c 24/3/19 受験勉強のコツです。 受験の数学で必須項目の一つに「三平方の定理」があります。 a 2 b 2 = c 2 です。 (ここで、直角に対する辺cが斜辺です。 ) 図1:直角三角形。 90゜に対する辺cが、斜辺。 さらに、応用問題でよく利用される辺の比があります。・円周角の定理の逆 三平方の定理 ・三平方の定理とその証明 ・三平方の定理を活用すること 標本調査 ・標本調査の必要性と意味 ・標本調査で母集団の傾向をとらえ説明 すること 関数 y=ax2 ・事象と関数 y=ax2 ・関数 y=ax2 の特徴 ・関数 y=ax2を 用いること




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学
三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。 今回は「直角三角形TOP7」と題して、三平方の定理にまつわるお話をしていきます。 三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。 非常に便利ですが、二次方程式になってしまうので解答するのに時間がかかります。 そこで、テストによく出てくる直角三角形については暗記してしまいましょう。 ここでは、特に6/1/15 解き方 PQ=31なので、P=3 〔kW〕、 Q=1〔kvar〕の直角三角形を作ります。 三平方の定理より、皮相電力S 〔kV・A〕は、 〔kV・A〕 電力の公式より、力率は、 ≒0949 無効率は、 ≒0316 力率とは有効電力と皮相電力の比、無効率とは無効電力と皮相電力の比の




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4




受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学
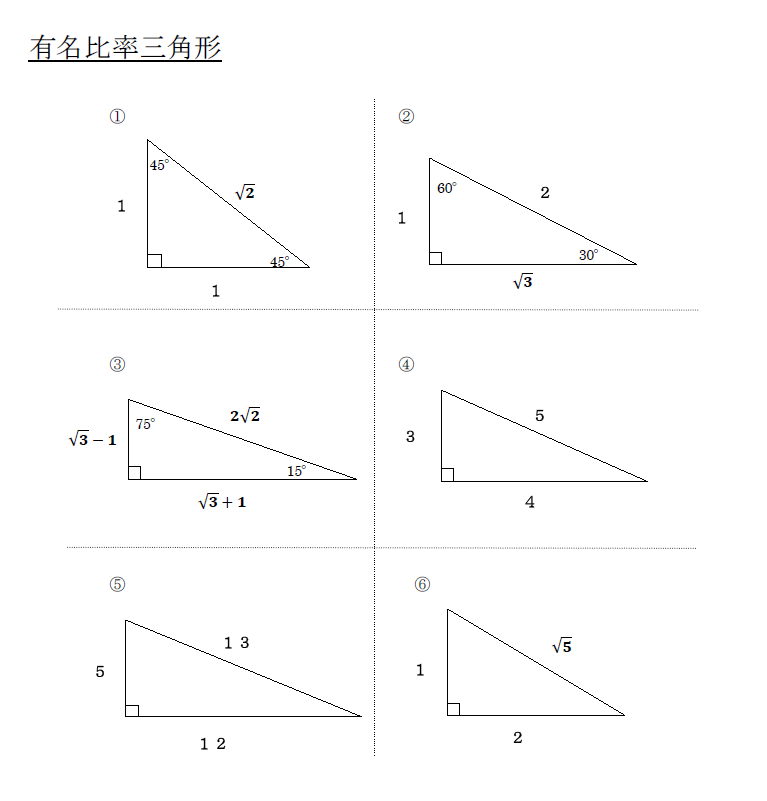
円錐の体積比を解説! 円周角の定理 円周角の定理 必須の問題10選を解説! 円周角の発展問題、円の中にブーメラン型! 三平方の定理 初めに覚えておきたい三平方の基本公式! 三平方の定理の逆ってなに?どうやって証明するの?や が出てくるのは,次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形 45°,45°,90°の 直角三角形 3辺の比は となり 三平方の定理(ピタゴラスの定理)を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x²




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
単 元 名 ページタイトル 単元別一括 1 式の計算 多項式と単項式の乗除(1) 問題一括 (10,051Kb) 解答一括 (11,805Kb) 覚えるだけで簡単に三平方の定理の計算問題が解けるよ。 覚えると便利!直角三角形の3つの比 それじゃあ早速、中学数学の問題でよく出てくる、 直角三角形の辺の比 を3つ紹介するよ。 比その1 「1 2 √3」 まず覚えておいておくべき直角三角形の辺の/8/21 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。




三平方の定理を使うのか 比の計算をするのか 見極め方がよくわかりません Clear




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube
三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



数学 三平方の定理を5秒で計算する裏ワザ 見ないと損する 予備校なら武田塾 京成佐倉校




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理で辺を求める Youtube




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
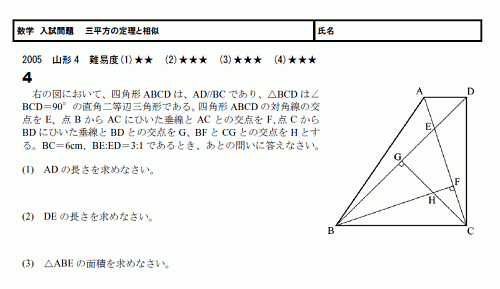



相似比の利用 三平方の定理 スタディーx



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
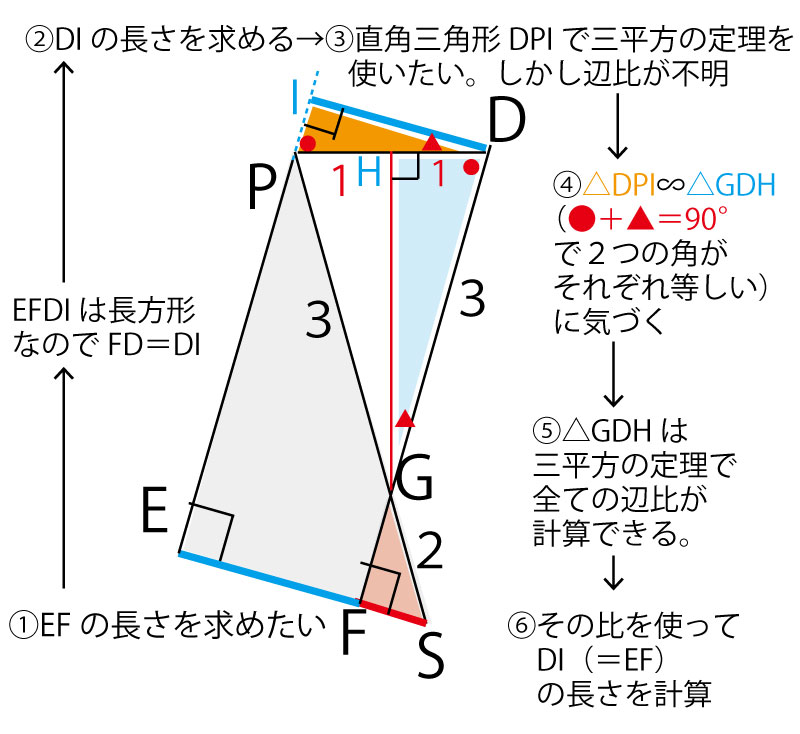



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora
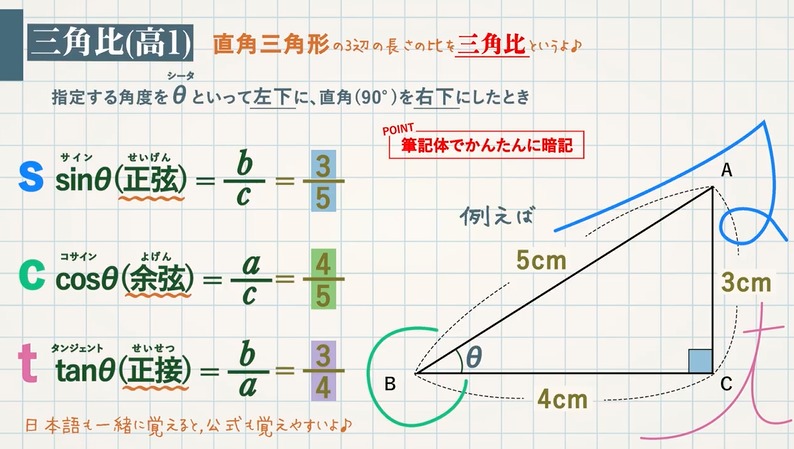



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 覚えておきたい基本公式を解説 数スタ




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理の証明と使い方




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも



三平方の定理 ピタゴラスの定理 考え方と答え めざせ 自給自足 改め 日々あれこれ
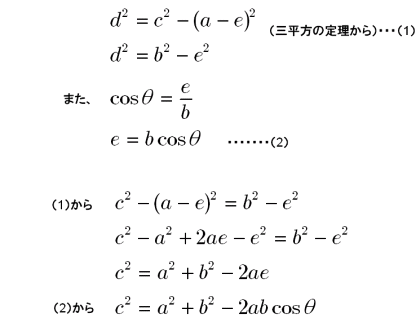



三角比 余弦定理 大人が学び直す数学




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ



3




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理の利用 四角錐 円錐 チーム エン




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
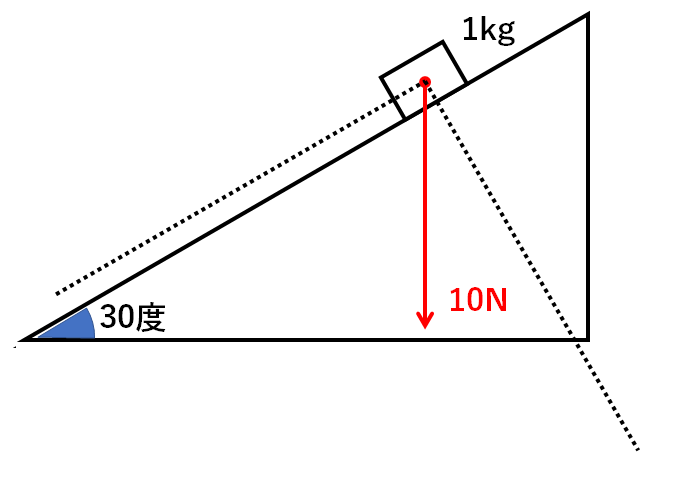



中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理




三平方の定理 覚えておきたい基本公式を解説 数スタ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三角比を用いた計算問題をマスターしよう スタディクラブ情報局




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく



1




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




三平方の定理 自動計算サイト



Studydoctor三平方の定理とよくある辺の比 中学3年数学 Studydoctor




三平方03 三平方の定理と比の計算 Youtube




わかりやすい三角比と基本公式 Irohabook
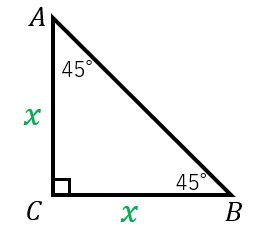



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




三平方の定理の証明と使い方




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理から円周率を計算してみる Yamav1 02bのブログ



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題




三平方の定理の証明と使い方




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



1




三平方の定理の証明と使い方




高校数学 三平方の定理による三角関数の計算 2 映像授業のtry It トライイット




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ



1




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三角比 30 45 60 もう一度やり直しの算数 数学



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理とよくある辺の比 中学3年数学 Youtube



Studydoctor三平方の定理の計算 中学3年数学 Studydoctor




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典



0 件のコメント:
コメントを投稿