Misc 8 Let A = 1−21−231115 verify that (i) adj A1 = adj (A1) First we will calculate adj (A) & A1 adj A = A11 A12 A13 A21 A22 A23 A31 A32 A33′= A11 A21 A31 A12 A22 A32 A13 A23 A33 A−5 Since cos(c) ≤1 and R 2n1(x) ≤ x2n2 (2n2)!Given the polynomial f (x) = 8 x 5

Solve The Following 5 1 2 1 3 1 4 Mathematics Topperlearning Com 1lw16x22
1 500 pesos to dollars
1 500 pesos to dollars- Ex 122, 1 Find the distance between the following pairs of points (i) (2, 3, 5) and (4, 3, 1) Let P be (2, 3, 5) and Q be (4, 3, 1) Distance PQ = √((x2−x1)2(y2−y1)2(z2 −z1)2) Here, x1 = 2, y1 = 3, z1 = 5 x2 = 4, y2 = 3, z2 = 1 PQ = √((4−2)2(3−3)2(1 −5)2) =562 04 Lecture #13 page 2 Note splitting between vibrational levels εvib (v1)−=εθvib (v) k vib Recall energy (cm1) ~ 2/3 T (K) 1 ν ≈−400 4 000 cm ⇔θvib ≈600−6 K So for almost all molecules at room T, θvib >T Not in highT limit!




Arithmetic Sequence Formula Chilimath
Is the product of all positive integers from 1 1 1 to n − 1 n1 n − 1, the product must contain d d d and thus be divisible by d d d So we have (n − 1)!Click here👆to get an answer to your question ️ Find the value of the polynomial 5x 4x^2 3 at x = 1, 2, 2The average of the yearly change between 0610 is 2515(−30) 4 Wrong Interpretation " The average rate of change of people who emigrated from Ireland is 00 people per year
Z{3,1,4,2,5} = 31z−1 4z−2 2z−3 5z−4 = 3z4 1z3 4z2 2z 5)/z5 Z{2δn7δn−23δn−5} = 27z−2 3z−5 = (2z5 7z3 3)/z5 (2) Recall that the underline in the first example shows the location of time n = 0 The second example can beClick here👆to get an answer to your question ️ Show that A = satisfies the equation A^2 3A 7I = 0 and hence find A^1See answer › Systems of equations 1 Solve the system 5 x − 3 y = 6 4 x − 5 y = 12 \begin {array} {l} {5x3y = 6} \\ {4x5y = 12} \end {array} 5x−3y=6 4x−5y=12 See answer ›
NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Again, cos y = √1−sin2 = √1−9 25 = 4/5 And tan y = sin y / cos y = ¾ Solve for tan(x y), using below identity,1 2 4 0 3 2 1 0 5 = −det 0 3 2 1 2 4 1 0 5 rows one and two interchanged det 1 2 4 0 3 2 1 0 5 = −det 1 4 2 0 2 3 1 5 0 columns two and three interchanged Corollary 41 If an n× n matrix has two identical rows or columns, its determinant must equal zero Proof The preceding theorem says that if you interchange any two rows or≡ 0 (m o d d) Also (n − 1)!




Suma Y Resta De Numeros Enteros Y Fracciones Profesor Moises Grillo Ppt Descargar



Http Www Math Utah Edu Macarthu Fall08 Math1010 Equationsolvingstrategies Pdf
27 If n is a positive integer then cos(nπ) = (−1)n Clearly 1 n1 < 1 n and lim n→∞ 1 n = 0 Therefore, the alternating series test implies that the series P cosnπ n converges 28 For n ≥ 3, the function f(n) = 1 2 n3 − 5 is positive;Lesson 28 Domain and Range of an Inverse Function 5 Example 2 List the domain and range of each of the following functions Then find the inverse function and list its domain and range a (𝑓𝑥)=−2 1−𝑥Given the polynomial f(x)=8x^5−5x^33x4, which one of the following is a possible rational root?




Ex 2 5 4 Solve X 5 3 X 3 5 Chapter 2 Class 8 Teachoo
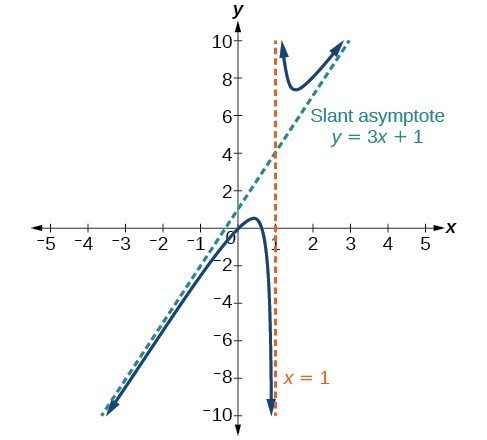



Identify Horizontal Asymptotes College Algebra
316 Explain the difference between average velocity and instantaneous velocitySECTION 71 INTEGRATION BY PARTS ¤ 5 30 Let =arctan(1 ), = ⇒ = 1 1(1 )2 −1 2 − 2 1, = By(6), √ 3 1 arctan 1 = arctan 2 f (− 1) = (− 1) 2 = 1 f(1)=(1)^2=1 f (− 1) = (− 1) 2 = 1 so we'll have an open dot at (− 1, 1) (1,1) (− 1, 1) and f (2) = 2 2 = 4 f(2)=2^2=4 f (2) = 2 2 = 4 so we'll have a closed dot at (2, 4) (2,4) (2, 4) The third piece is the horizontal linear function of f (x) = 4 f(x)=4 f (x) = 4 from x = 2 x=2 x = 2 to infinity What




9 3 Solve Using Square Roots Ppt Download




Global Regional And National Incidence Prevalence And Years Lived With Disability For 328 Diseases And Injuries For 195 Countries 1990 16 A Systematic Analysis For The Global Burden Of Disease Study 16 The Lancet
26E Exercises for Section 25 In exercises 1 4, write the appropriate ε − δ definition for each of the given statements The following graph of the function f satisfies lim x → 2f(x) = 2 In the following exercises, determine a value of δ > 0 that satisfies each statement 5) If 0 < x − 2 < δ, then f(x) − 2 < 11 Compute T(−4,5,1) Solution T(−4,5,1) = (2∗(−4)5,2∗5−3∗(−4),−4−1) = (−3,22,−5) 2 Compute the preimage of w = (4,1,−1) Solution Suppose (v1,v2,v3) is in the preimage of (4,1,−1) Then (2v1 v2,2v2 −3v1,v1 −v3) = (4,1,−1) So, 2v1 v2 = 4 2v2 −3v3 = 1 v1 −v3 = −1 The augmented matrix of this system315 Describe the velocity as a rate of change;




Finding Linear Equations
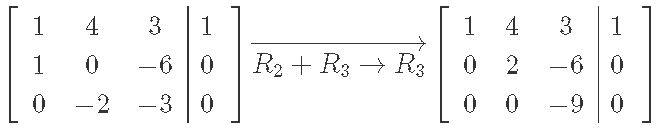



Systems Of Linear Equations Gaussian Elimination Studypug
Find the product 1 2 (5 − 2 i) 1 2 (5 − 2 i) Multiplying Complex Numbers Together Now, let's multiply two complex numbers We can use either the distributive property or more specifically the FOIL method because we are dealing with binomials Recall that FOIL is an acronym for multiplying First, Inner, Outer, and Last terms together≡ 0 ≡ − 1≤10−5 which is satisfied when n≥3 Hence cos(x) ≈1− x2 2!



1



Q Tbn And9gcrixojurqup9lk6wbiqccdlx3v8eo1g4a2y4gfl2xjzdcwg1hoi Usqp Cau
Lamb E (14), "Does 123Really Equal –1/12?", Scientific American Blogs This Week's Finds in Mathematical Physics (Week 124), , , Euler's Proof That 1 2 3 ⋯ = −1/12 – by John Baez;≤10−5 we must have π 4 2n2 (2n2)! Tanner Stage 5 334−1370 Female Ranges
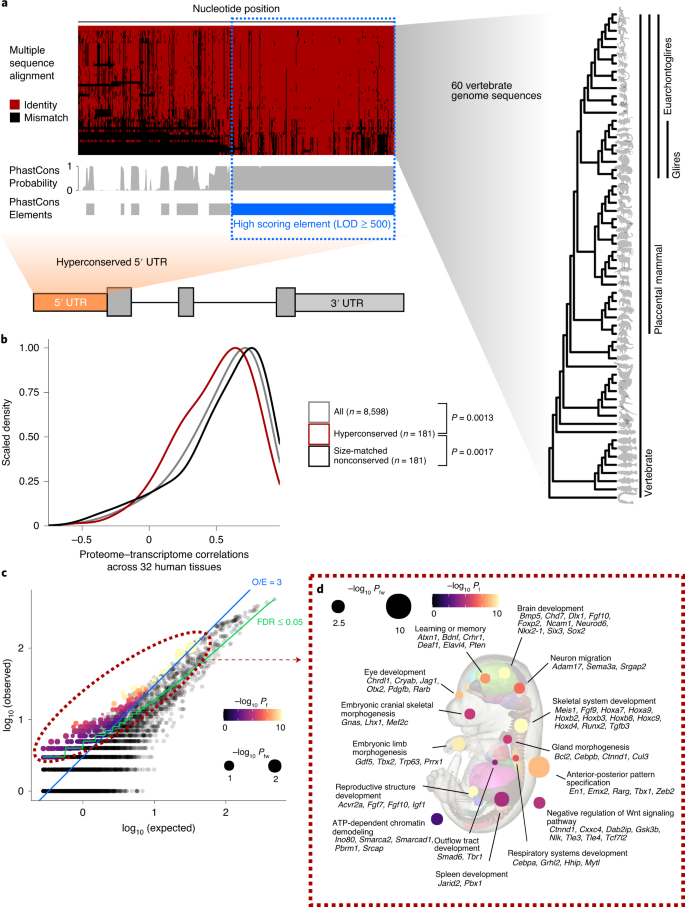



Functional And Structural Basis Of Extreme Conservation In Vertebrate 5 Untranslated Regions Nature Genetics



Factoring Trinomials Bingo
Solve each system Write your solution as an ordered pair, or indicate if it has no solutions, or infinitely many solutionsTherefore, detP = ((−1)n/2 if n is even (−1)n−1 2 if n is odd 1 if n 4 has remainder 0 or 1 −1 if n 4 has remainder 2 or 3 3 Problem 428 Show how rule 6 (det = 0 if a row is zero) comes directly from rules 2 and 3 Answer Suppose A is an n×n matrix such that the ith row of A is equal to zero45 POWER SERIES 97 45 Power Series A power series is a series of the form X∞ n=0 c0x n = c 0 c1xc2x 2 ···c nx n ··where x is a variable of indeterminate It can be interpreted as an infinite polynomial The cn's are the coefficients of the series The sum of the series is a function f(x) = X∞ n=0 c0x n




In A Survey Of 25 Students It Was Found That 15 Had Mathematics 12 Had Taken Physics And 11 Had Taken Chemistry 5 Had Taken Mathematics And Chemistry 9 Had Taken Mathematics




Ejercicios De Matrices Superprof
18, 9 f(x) = a(x−1)2 and 4a = 3 Thus f(5) = 3 4 42 = 12 15 24 24, 64 The bead was initially 13 inches below the level of her hands When it has moved up 8 inches, it will be 5 inches below the level of her hands, and will be 13 inches from each hand Thus each hand will have moved 12(=9) −3 24 − 3 2 2 2 10) −3 45 − 5 2 2 1 ©4 Z2L0F1 e27 5Kiu Etta P NSjoTf 5tqw oaFr 8e6 eL yL4C X OArl al t Frvi sg PhOtMso Yr7ensJe6rtv ne5dP2 9 JM Zafd le3 Mwsi kt HhX kI6nKf Li8nUiZtfe X TGIeYoSmOe Rt4r jy o c Worksheet by Kuta Software LLC Evaluate limx → 103x − 5 −−−−−√ 5limx → 103x − 55 1 Which of the following are integer values of x that will make the statement x>4 and x 5,6,7,8 Determine whether the graph is continuous or not continuous Not Continuous If x divides 49, then x divides 30




Suma Y Resta De Numeros Enteros Y Fracciones Profesor Moises Grillo Ppt Descargar




5 9 7 8 5 4 1 3 4 35 1 5 Gauthmath
8/15/19 JO AA Explanation of Changes E of C−1 Flight Services Explanation of Changes Basic Direct questions through appropriate facility/service center office staff312 Calculate the slope of a tangent line;≡ 0 (m o d d) (n1)!\equiv 0\pmod d (n − 1)!




The Set Ordered From Least To Greatest Is A 7 Gauthmath




Raiz Cuadrada De Cinco Wikipedia La Enciclopedia Libre
313 Identify the derivative as the limit of a difference quotient;1 is −2/5 times the second entry x 2 Thus all solutions of this equation can be characterized by 2t −5t = t 2 −5 , 2 where t is any real number The nonzero vectors x that satisfy Ax = −3x are called eigenvectors associated with the eigenvalue λ = −3 One such eigenvector is u 1 = 2Determine the product −444−7135−3−1 1−111−2−2213 and use it to Solve the system of equations x y z = 4 , x 2y 2x = 9 , 2x y 3z = 1




Rd Sharma Solutions For Class 6 Chapter 5 Negative Numbers And Integers Free Pdf




5 4 5 2 3 4 5 1 2 1 5 Gauthmath
Learning Objectives 311 Recognize the meaning of the tangent to a curve at a point;If k5Pk1 = 11k−12 k3Pk then the values of k are 7 Please scroll down to see the correct answer and solution guide−3 1 = 0 0 = 0 −3 1 λ= 5 We want to find those vectors xsuch that (A−5I 2)x= 000 This leads to the equation 2 6 1 3 −5 1 0 0 1 x 1 x 2 = 0 0 The coefficient matrix of this system, −3 6 1 −2 , is row equivalent to the matrix 1 −2 0 0 Any solution of this system satisfies x 1 = 2x 2 Hence, ker(A−




Solve The Following 5 1 2 1 3 1 4 Mathematics Topperlearning Com 1lw16x22



Multiplicative Inverse Wikipedia
185 (d) Find all real values x such that 2x1 x−5 ≤ 3 We consider the cases x ≥ 5 and x < 5 separately If x ≥ 5, the inequality becomes 2x 1 ≤ 3(x − 5), which is equivalent to x ≥ 16 If x < 5, then we get 2x 1 ≥ 3(x − 5), leading to x ≤ 16 From the first case we get all x ∈ 16,∞), from the second case we get all0 0 1 0 0 7 7 0 0 4 2 0 7 0 5 6 8 − 1 Calculate to the power of 1 and get \frac{}{} Calculate 0 0 1 0 0 7 7 0 0 4 2 0 7 0 5Exam 1 Review Questions and Answers Part I Finding solutions of a given differential equation 1 Find the real numbers r such that y = ex is a solution of y00 −y0 − 30y = 0 Answer r = 6, −5
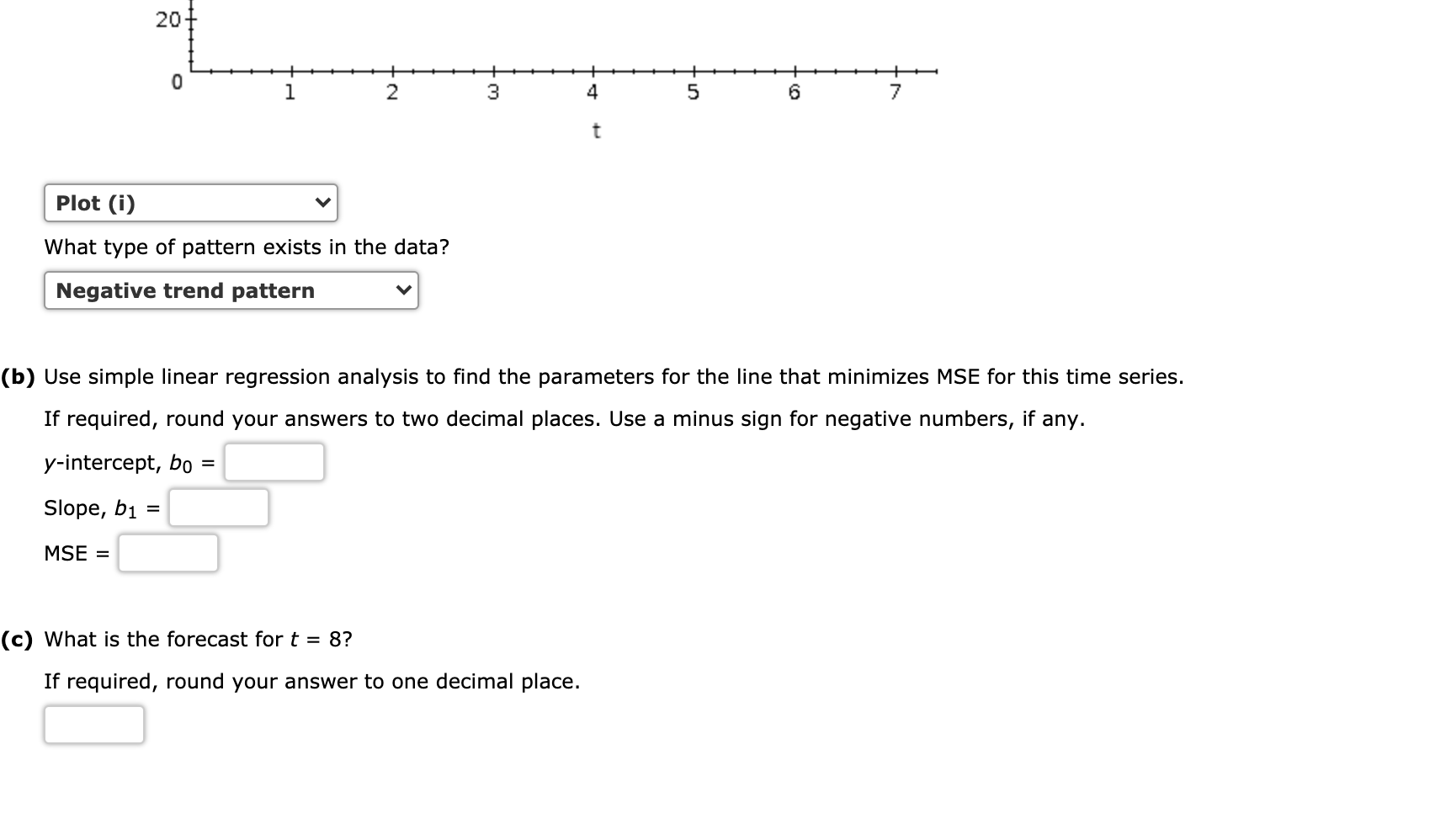



Consider The Following Time Series T 1 2 3 4 5 6 7 Chegg Com




Operaciones Combinadas Ppt Descargar
314 Calculate the derivative of a given function at a point;F′(n) = 3 2 n2 is positive and f(3) = 27 2 − 5 > 0 Adding 1 2 n3 to both sides of theN=1 (− n 5)n Solution Note that this is an alternating series where b n = n 5 n If we first look at lim n→∞ b n we see that lim n→∞ n 5 n = ∞ since we have that lim n→∞ n 5 = ∞ Thus by the alternating series test we have shown that the series DIVERGES Note that using the Root test from 116 gives you the same result




Bernoulli Number Wikipedia



Microsoft Math Solver Math Problem Solver Calculator
1 10−5 1 10−3 001 sin e001 −1 −sin e−001 −1 2 001 1 − sin e001 −1 −sin e−001 −1 2 001 1 10−9 8 10−7 ii f ′′ x ex cos ex −1 −e2x sin ex −1 , f ′′ 0 1 f ′′′ x ex −e3x cos ex −1 −3e2x sin ex −1≡ 0 ≢ − 1 (m o d d) (n1)!\equiv 0\not\equiv 1\pmod d (n − 1)!4 12 Since first became available to the public in mid05, the rate at which video has been uploaded to this site can be approximated by ( )=11 2−26 23 million hours of videos per year (0≤ ≤9), where is time in years since June 05




Rd Sharma Solutions For Class 6 Chapter 5 Negative Numbers And Integers Free Pdf




Rectangular Coordinate System
Page 5 (Section 41) 41 Homework Problems 1 Use a calculator to find each value to four decimal places (a) 5 (b) 3 7 (c) π 2− 53 (d) e2 (e) e−2 (f) −e 025 (g) π−1 2 Simplify each expression without using a calculator The LibreTexts libraries are Powered by MindTouch ® and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot We also acknowledge previous National Science Foundation support under grant numbers ,− 10 ≤ t ≤ 10 − 10 0 10 − 1 − 05 0 05 1 t f(t) write f as a product f (t)= g (t)cos t where g is a rectangular pulse of width (see page 127) F




Slope Intercept Form Introduction Algebra Article Khan Academy




Ex 2 1 1 Solve I 2 3 5 Ii 4 7 8 Iii 3 5 2 7
Question Suppose u=〈3,3,−1〉u=〈3,3,−1〉 and v=〈−5,1,−1〉v=〈−5,1,−1〉 Then The projection of uu along vv is The projection of uu orthogonal to vv is Let A=⎡⎣⎢2−214−34⎤⎦⎥A=24−2−314 Find an orthonormal basis of the image of A Find the orthogonal projection of v=⎡⎣⎢−2−144⎤⎦⎥v−10 −9 −8 −7 −6 −5 −4 −3 −2 −1 0 1 Real Axis b The asymptotes By rule 5, (−4 − 3 − 2 − 0) − (−1) 8 σa = = − , 4 − 1 3 (2m 1)π π 5π θa = =,π, 4 − 1 3 3 c The value of gain that makes the system marginally stable By rule 7, setting G(jω)=−1, we find K(jω 1) = −1P −1/2 ≤ X < 3/4 = P −1/2 < X ≤ 3/4P X = −1/2 −P X = 3/4 (3) Since the CDF of X is a continuous function, the probability that X takes on any specific value is zero This implies PX = 3/4 = 0 and PX = −1/2 = 0 (If this is not clear at this point, it



Perfect Cubes And Cube Roots Video Lessons Examples And Solutions



Sd0ne3t9z6mvem
John Baez () "My Favorite Numbers 24" (PDF) The EulerMaclaurin formula, Bernoulli numbers, the zeta function, and realvariable analytic continuation by Terence Tao−1/10 1/5 1 1 1 1 −1 0 1 2 2 0 −3 −5 = 3/10 −1/10 −1/10 1/5 −6 −15 = −3/10 −12/5 Therefore, the bestfit line for the data is y = − 3 10 − 12 5 t Here's a plot of both the data and the bestfit line75 5 25 0 25 5 75 25 5 5 Problem 3325 Suppose that




Finding Linear Equations




Raiz Cuadrada De Cinco Wikipedia La Enciclopedia Libre




Purification And Characterization Of Hypoxia Inducible Factor 1 Journal Of Biological Chemistry




Complex Numbers Absolute Value




Nedis Cvgtbk15 Scart Cable 1 5 M Lampamania




Problemas Resueltos De Disoluciones



Identify Horizontal Asymptotes College Algebra




If A 5 7 B 4 5 C 1 6 And D 4 5 Are Vertices Of Quadrilateral Find Of The Quadrilateral Abcd Maths Coordinate Geometry Meritnation Com




Multiplying And Dividing Radical Expressions




Finding Linear Equations




Ex 2 5 1 Solve X 2 1 5 X 3 1 4 Chapter 2 Class 8




Distributive Property




5 9 3 5 3 5 Evaluate The Above Question The Two Minus Signs Are With The Two Powers 2 And Brainly In




Ex 2 1 1 Solve I 2 3 5 Ii 4 7 8 Iii 3 5 2 7
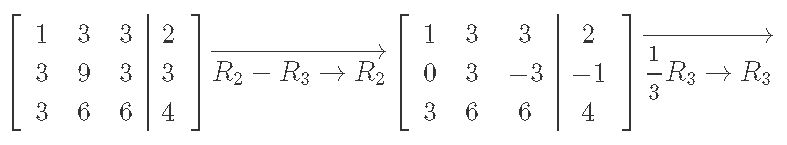



Systems Of Linear Equations Gaussian Elimination Studypug



Z Scan Curves For M 4 And Different Values Of F 0 Z 0 5 Point 1 Download Scientific Diagram




Finding Linear Equations
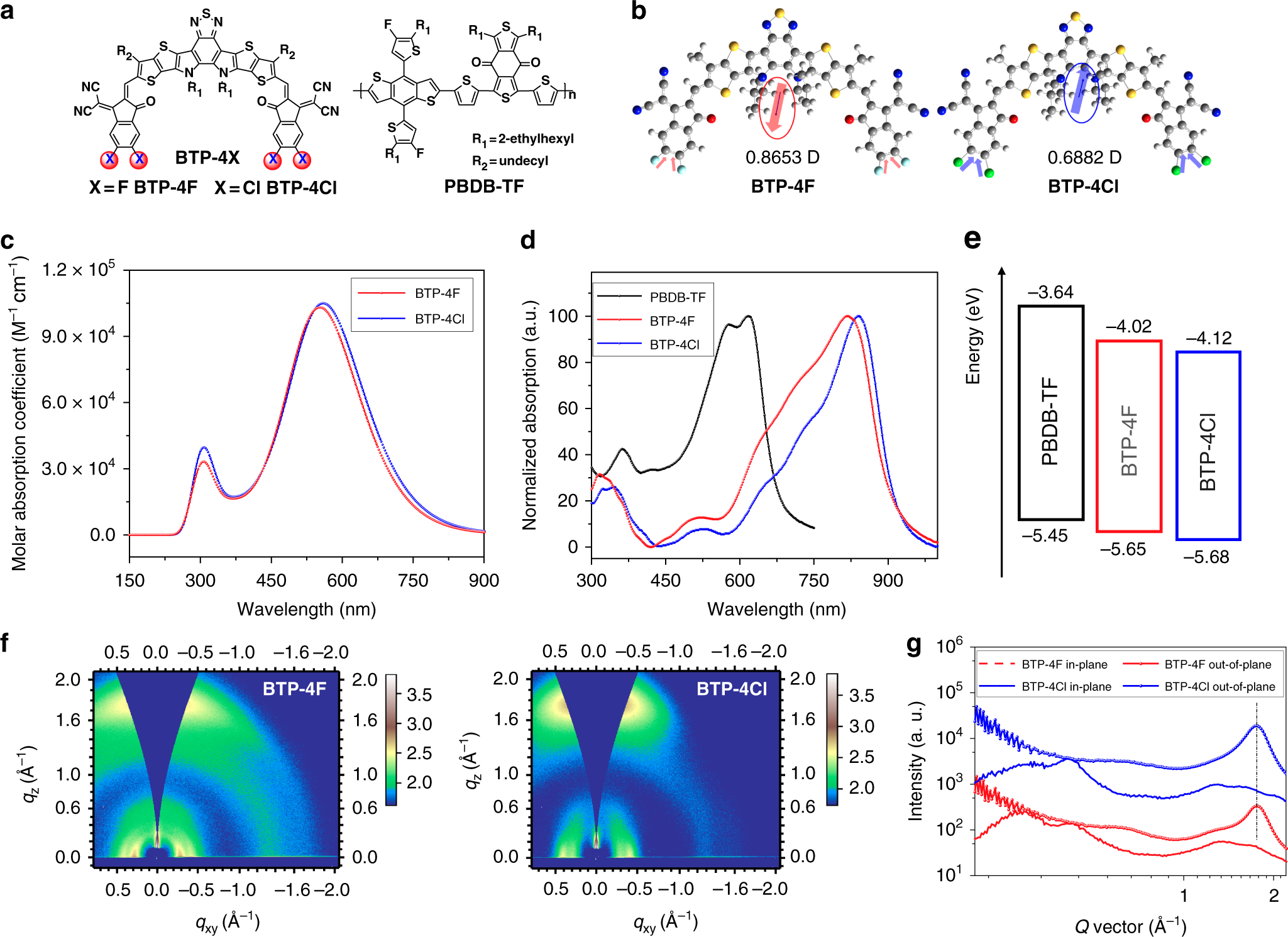



Over 16 Efficiency Organic Photovoltaic Cells Enabled By A Chlorinated Acceptor With Increased Open Circuit Voltages Nature Communications




Operaciones Combinadas Ppt Descargar




Respuesta De 18 1 3 1 5 Brainly Lat



Sodium Mod 1 16 5 1 16 1 Boost Your Fps 9minecraft Net




Ejercicios De Matrices Superprof




Evolution Of Scalar Field For Higgs Potential For Lfor For L 1 M Download Scientific Diagram




Fractions To Decimals Teachertwins C Ppt Download




Align Numbers In Table With Scientific Notation And Minus Sign Tex Latex Stack Exchange




Hypofractionated Breast Radiotherapy For 1 Week Versus 3 Weeks Fast Forward 5 Year Efficacy And Late Normal Tissue Effects Results From A Multicentre Non Inferiority Randomised Phase 3 Trial Sciencedirect




Answered Use The Fact That 1 1 X N 0 To Obtain A Bartleby



1




Ecuaciones Con Propiedades De Logaritmos Ppt Descargar
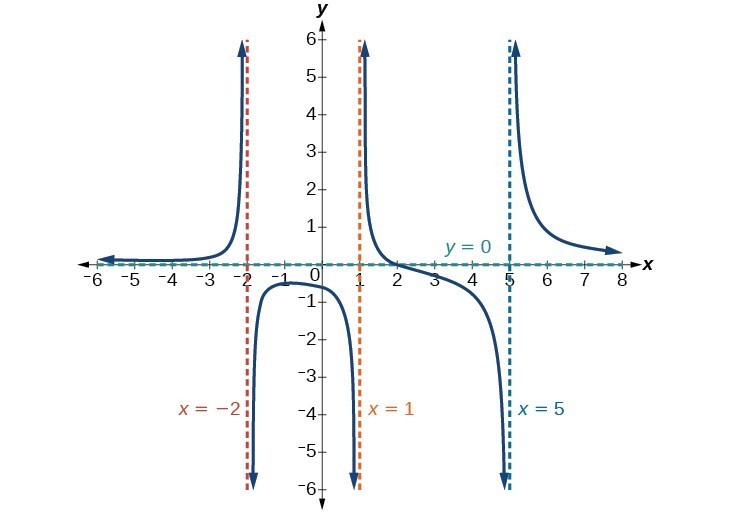



Identify Horizontal Asymptotes College Algebra




Ex 4 1 7 I Class 12 Find Values Of X If Determinants




Algebra




Inequity In Consumption Of Goods And Services Adds To Racial Ethnic Disparities In Air Pollution Exposure Pnas



Http Www2 Chem Uic Edu Tak Chem Solutions set 6 Pdf
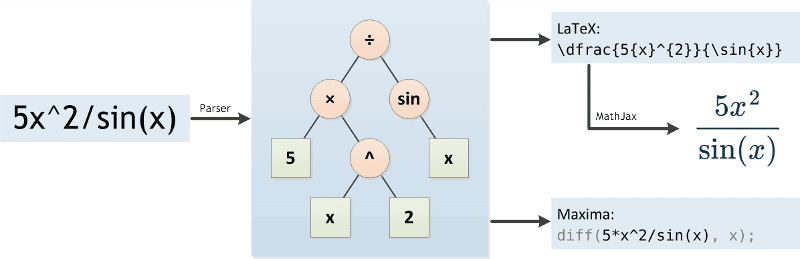



Derivative Calculator With Steps




Algebra Calculator Mathpapa



Q Tbn And9gct C2b9wlkbzawy4rdjkghqtr Zyvinxjxrzym9wwegbkvlpj Usqp Cau
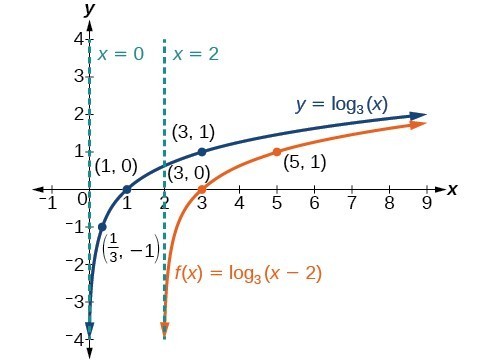



Graphing Transformations Of Logarithmic Functions College Algebra




Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra




Ejercicios De Matrices Superprof




Ex 4 6 15 If A 2 3 5 3 2 4 1 1 2 Find A 1 And Solve




C R I Q I Z N Los Numeros Complejos A Bi Ppt Descargar




The Following Sample Observations Were Randomly Chegg Com
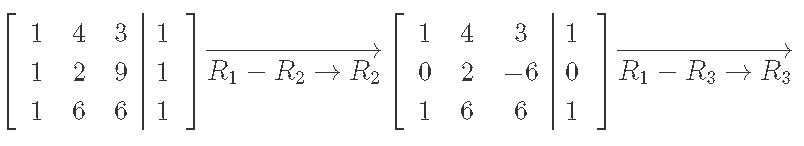



Systems Of Linear Equations Gaussian Elimination Studypug




Arithmetic Sequence Formula Chilimath




Ex 2 1 1 Solve I 2 3 5 Ii 4 7 8 Iii 3 5 2 7




Ex 4 6 15 If A 2 3 5 3 2 4 1 1 2 Find A 1 And Solve



Microsoft Math Solver Math Problem Solver Calculator




Mrs Rivas Ppt Download
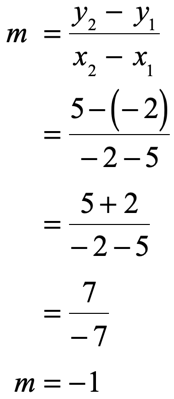



Slope Intercept Form Of A Straight Line Y Mx B Chilimath
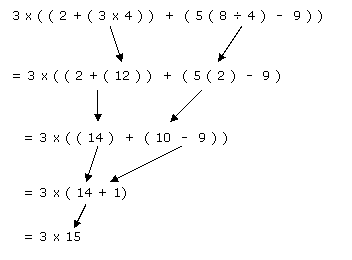



Order Of Operations




Example 4 Find 2x2 6x X2 1 Dx And Chegg Com




Ex 2 1 1 Solve I 2 3 5 Ii 4 7 8 Iii 3 5 2 7




Lego Tile 1 X 2 X 5 6 With Stud Hole In End With Black Pattern Hyphen Minus Sign Brick Owl Lego Marketplace




Problemas Resueltos De Disoluciones




Find Slope And Y Intercept From Equation Process Expii




Raiz Cuadrada De Cinco Wikipedia La Enciclopedia Libre



Resuelvela Siguiente Operacion Combinada 1 4 5 2 8 3 1 6 Brainly Lat
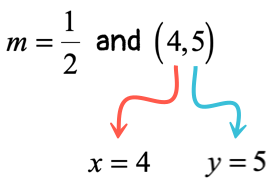



Slope Intercept Form Of A Straight Line Y Mx B Chilimath



Www Macmillaneducation Es Wp Content Uploads 18 10 Cientifico Matematico Advantage Multimedia Pdf




Studio One 5 Prime Presonus Shop




0 4 0 5 Operations With Fractions Ppt Download



Studio One 5 Prime Presonus Shop




Dementia Prevention Intervention And Care Report Of The Lancet Commission The Lancet




Problem Set 1 Solution Che 4163 Transport Phenomena And Numerical Methods Problem Set Problem Vector Has Components Vx Vy Vz Vector Has Components Wx Wy Wz Studocu




Problemas Resueltos De Disoluciones




Ejercicios Resueltos De Inecuaciones Cuadraticas




Ejercicios De Matrices Superprof



If 2x 1 What Is X In Decimals Quora




1 Efetue As Seguintes Divisoes A 15 5 I 75 5 Gauthmath




Solutions To Homework Assignment 5
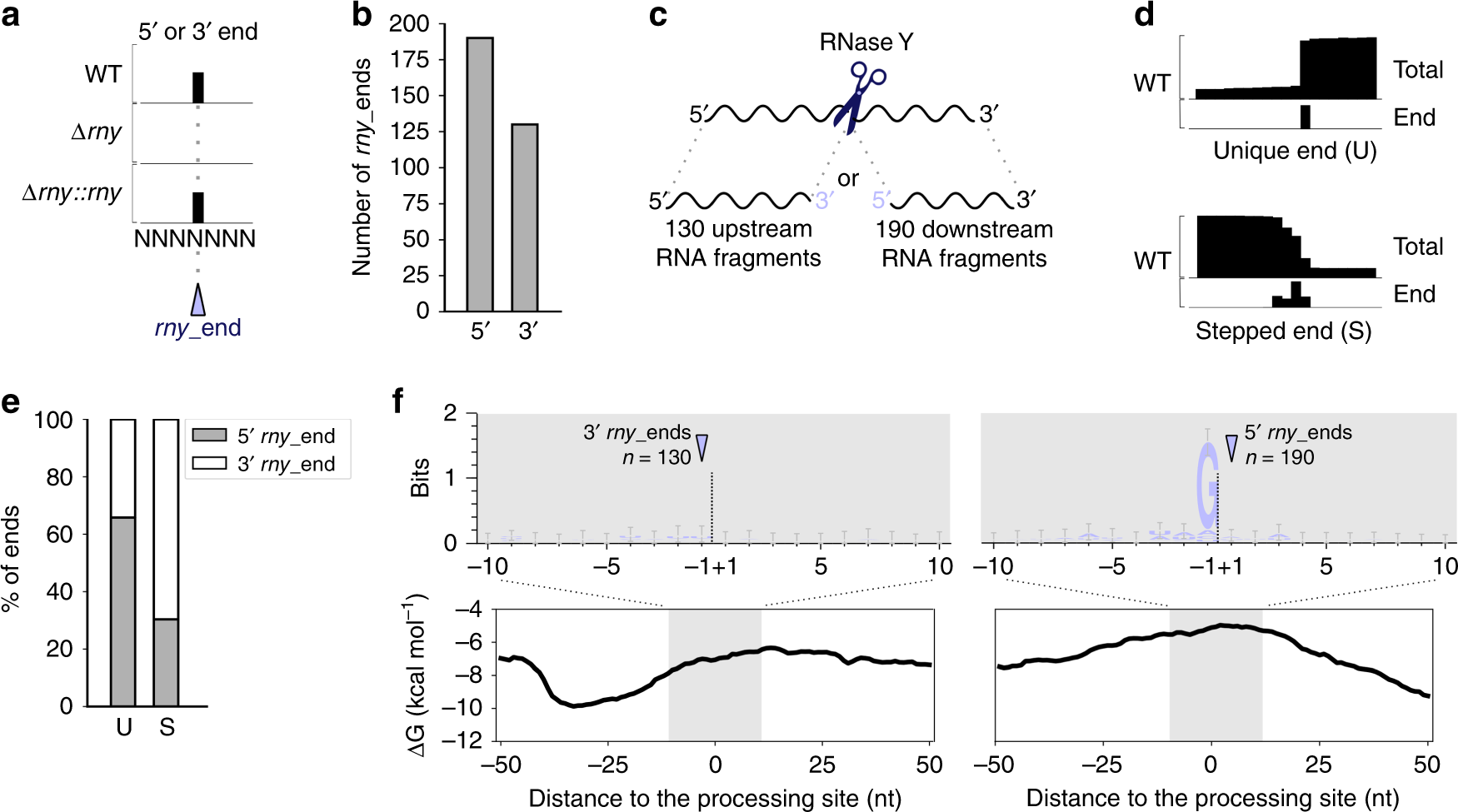



An Rna Seq Based Comparative Approach Reveals The Transcriptome Wide Interplay Between 3 To 5 Exornases And Rnase Y Nature Communications



0 件のコメント:
コメントを投稿