In this video explaining vtu engineering mathematics third semester problemThis problem is second degree finding a, b and c parametersThis method is very iThe equation is y = ax^2 bx c the y intercept is the value of y when the value of x is 0 when the value of x is 0, this equation becomes y = a*0 b*0 c which becomes y = c there is only 1 value of c that can satisfy this equation, and that is the value of c that is given at the start of the equation example y = x^2 30x 15Y = ax2 bxc;
Quadratic Graph Example Y Ax C Expii
What is a in y=ax^2+bx+c
What is a in y=ax^2+bx+c-Learn termquadratics = y = ax^2 bx c with free interactive flashcards Choose from 68 different sets of termquadratics = y = ax^2 bx c flashcards on QuizletFactoring ax2 bx c This section explains how to factor expressions of the form ax2 bx c, where a, b, and c are integers First, factor out all constants which evenly divide all three terms If a is negative, factor out 1 This will leave an expression of the form d (ax2 bx c), where a, b, c, and d are integers, and a > 0



Quadratic Graph Example Y Ax Expii
Y ax2 bx c 0 Example • Graph y = 25x Example • Graph y = 3x 1 Then state the yintercept Example • Graph y = 5x – 4 Then state the yintercept Growth and Decay • Exponential functions are used to represent situations of exponential growth and decayComplete info about it can be read hereB is the yintercept to convert from the standard form of the equation of ) your slope of m is equal to (a/b) your yintercept of b is equal to (c
Factor Form y=a (xr) (xs) Zeros or xintercepts (r and s) Axis of Symmetry (x= (xs)/2) Optimal value (sub in) Standard Form y=ax^2bxc Zeros Axis of symmetry (b/2a) Completing the square to turn to vertex Factoring to turn to factored formY = ax2 2ahx ah2 k Use the Distributive Property This is in standard form, with b = –2ah and c = ah2 k With these substitutions, the equation becomes y = ax2 bx c Congruent Parabolas Because the parabola determined by the equation y k = a(x h)2 is a translation image of the parabola determined by the equation y = ax2, the two parabolas are congruentAx b(0) = c x = c/ , 0) The y intercept is found by setting x = 0 in the above equation and solve for x a(0) by = c y = c/b Hence, the y intercept is at (0 , c/b) Example Find the x and y intercepts of the graph of the equations given below 2x y = 2 4x 2y = 0
Suppose you have ax 2 bx c = y, and you are told to plug zero in for yThe corresponding xvalues are the xintercepts of the graph So solving ax 2 bx c = 0 for x means, among other things, that you are trying to find xinterceptsSince there were two solutions for x 2 3x – 4 = 0, there must then be two xintercepts on the graphGraphing, we get the curve belowTrinomials of the Form ax^2 bx c Study this pattern for multiplying two binomials Example 1 Factor 2 x 2 – 5 x – 12 Begin by writing two pairs of parentheses For the first positions, find two factors whose product is 2 x 2 For the last positions, find two factors whose product is –12 Following are the possibilitiesX2 x1 1 x2 2 x2 1 x2 n xn 1 a b c = y1 y2 yn or, in other words, the system



1
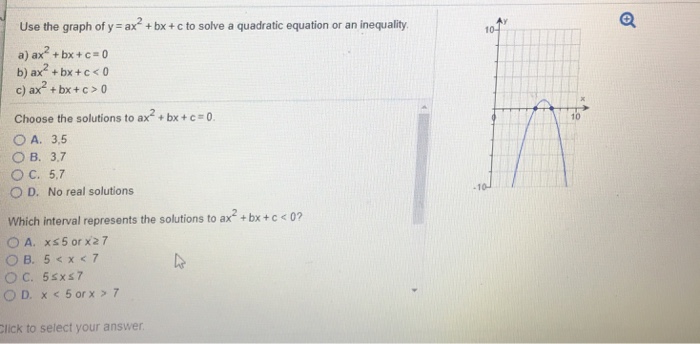



Use The Graph Of Y Ax 2 Bx C To Solve A Chegg Com
Synthetic division by a x 2 b x c I know that synthetic division can be used in order to find quotient q ( x) and remainder r ( x) of a polynomial p ( x) when it is divided by some linear polynomial like x − c Now, does exist some procedure (another than long division) in order to find q ( x) and r ( x) when the divisor is a x 2 b x c?Hi Elliot The inverse of a function f is a function g such that g(f(x)) = x So if you have the function f(x) = ax 2 bx c (a general quadratic function), then g(f(x)) must give you the original value xYou should already see the problem there will be two functions, not one, since a function must provide a unique value in its range for each value in its domain and a quadratic maps twoExample 1) Graph y = x 2 2x 8 In this problem a = 1, b = 2 , and c = 8 Since "a" is positive we'll have a parabola that opens upward (is U shaped) To find the xintercepts we plug in 0 for y 0 = x 2 2x 8 (which factors) 0 = (x 4)(x 2) x = 4 or x = 2 So this parabola has two xintercepts (4,0) and (2,0)



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




Graphing Quadratic Functions Y Ax 2 Bx C
X = 4/(2*1) x = 2 the y coordinate of the vertex can be computed by inserting 2 for x in the quadratic function y = x² 4x 12 y = (2)² 4*(2) 12 y = 4 8 12 y = 16 the coordinates of the vertex are vertex = (2, 16) The vertex of this parabola is a minimum point There is no maximum pointIf b 24ac < 0, the equation has no real roots and the parabola does not intercept the xaxis;Example of how to calculate the roots of a quadratic equation Find the zeros of the function f(x) = x 2 – 5x 6 Solution If a = 1 b = – 5 c = 6



Quadratics




Find The Values Of X That Give Critical Points Of Y Chegg Com
The general form of a quadratic is "y = ax 2 bx c"For graphing, the leading coefficient "a" indicates how "fat" or how "skinny" the parabola will beFor a > 1 (such as a = 3 or a = –4), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values y=ax^2 bx c y'=2ax b y''=2a y'''=0 So, the Wrosnkian would be y x^2 x 1 y' 2x 1 0 y'' 2 0 0 y''' 0 0 0 Which leads to 2y'''=0 Is that correct?Formula & Examples Formula The equation is y = a bx cx2 and the normal equations are 1 ∑y = an b∑x c∑x2 2 ∑xy = a∑x b∑x2 c∑x3 3 ∑x2y = a∑x2 b∑x3 c∑x4 Examples 1 Calculate Fitting a second degree parabola Curve fitting using Least square method




Graphing Y Ax 2 Bx C



Exploring Parabolas Y Ax 2 Bx C
What does Y ax 2 bx c represent?For some constants a, b, and c This means that all our plotted data points should lie on a single parabola In other words, the system of equations below should have exactly one solution ax2 1bx1 c = y1 ax2 2 bx2 c = y2 ax2 n bxn c = yn! y = ax^2 bx c differentiating with respect to X dy/dx =2ax b 5 examples of newton first law of motion Report the answers to my questions Choose the correct synonyms of the underlined word In spite of his problems, he seems quite unruffled a) gathered b) possessed c) relaxed d) detached




Factoring Trinomials Of The Form Ax 2 Bx C




Quadratic Graph Example Y Ax Expii
The curve `y=ax^(3)bx^(2)cx5` touches the xaxis at `P(2,0)` and cuts the yaxis at a point Q where its gradient is 3 Find a,b,cWelcome to Doubtnut DoThe red graph is y = ax2 bx c y = ax 2, the basic parabola will always be in red in future examples for comparison purposes Notice that when the value for variable 'a' is positive, the minimum of the graph does not change even though the value for variable 'a' was changed if b 24ac = 0, the equation has two equal real roots and the parabola is tangent to the xaxis (x1 = x2);



Graphing Quadratic Functions Y 2 Ax Bx C




Form The Differential Equation From The Following Primitives Where Constants Are Arbitrary Y A X 2 B X C
Given that mathy=axbx^2/math math\frac{dy}{dx}=y'=a2bx/math math\frac{d^2y}{dx^2}=y''=2b/math then mathy=x\,y'\frac{1}{2}x^2 y"/mathIf the graph of the quadratic function \(y = ax^2 bx c \) crosses the xaxis, the values of \(x\) at the crossing points are the roots or solutions of the equation \(ax^2 bx c = 0 \) IfThe equation `y=ax^2bxc` is a means of describing the quadratic function If a quadratic function is equal to zero, the result will be a quadratic equation with



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
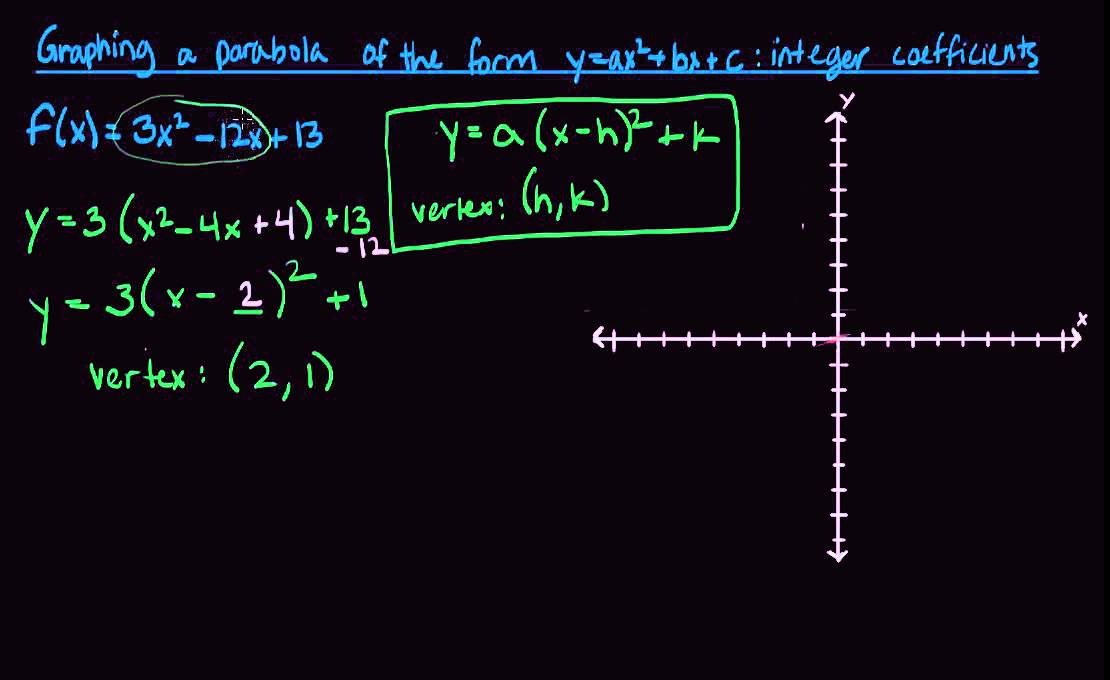



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
The term quadratic comes from the word quadrate meaning square or rectangular Thus, the standardized form of a quadratic equation is ax2 bx c = 0, where "a" does not equal 0 Note that if a = 0, the x2 term would disappear and we would have a linear equation!Every quadratic has a (single) yintercept The reason for this is that the yintercept is the function value at x = 0, and we can always substitute x = 0 into the quadratic Thus, the yintercept of the quadratic function y = ax 2 bx c is c For the other forms of the function, just substitute x = 0 to find the corresponding value of y The graph of the quadratic y = ax^2 bx c has the following properties (1) The maximum value of y = ax^2 bx c is 5, which occurs at x = 3 (2) The graph passes through the point (0,13) If the graph passes through the point (4,m), thenY = ax 2 bx c A suitable conclusion statement from such a relationship would be that y is quadratic with x y



Exploring Parabolas Y Ax 2 Bx C
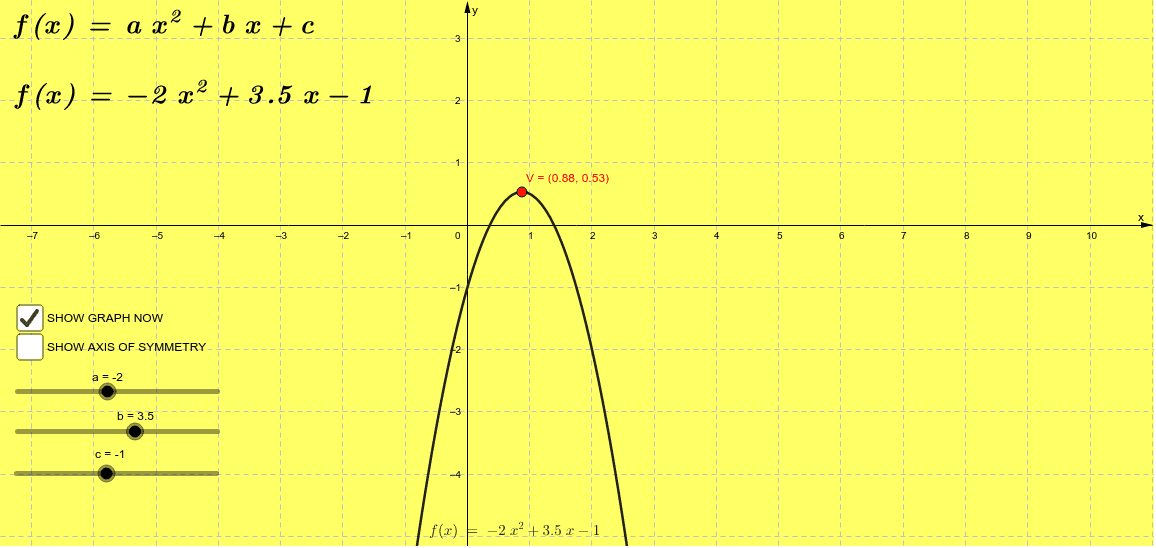



The Quadratic Function Y Ax2 Bx C Geogebra
How to Graph a Parabola of the Form {eq}y=x^2 bx c {/eq} Example 1 Our quadratic equation is {eq}y = x^2 2x 3 {/eq} Step 1 First we need to find the vertex of our parabolaSolve for a y=ax^2bxc y = ax2 bx c y = a x 2 b x c Rewrite the equation as ax2 bx c = y a x 2 b x c = y ax2 bxc = y a x 2 b x c = y Move all terms not containing a a to the right side of the equation Tap for more steps Subtract b x b x from both sides of the equationAbout Graphing Quadratic Functions Quadratic function has the form $ f(x) = ax^2 bx c $ where a, b and c are numbers You can sketch quadratic function in 4 steps I will explain these steps in following examples




Graphing Quadratic Functions Of The Form Y Ax 2 Bx C Example 2 Video Algebra Ck 12 Foundation



Exploring Parabolas Y Ax 2 Bx C
Graphing quadratic functions in standard form y = ax^2 bx c, by converting them to vertex formClick here👆to get an answer to your question ️ The graphs of y = ax^2 bx c are given in Figure Identify the signs of a, b and c in each of the following Join / Login maths The graphs of y = a x 2 b x c are given in Figure Identify the signs of a, b and c in each of the following An equation is simply an expression with two equal terms For example y = ax 2 bx c If the quadratic equation meets the requirement for functions (that each input is matched to at most one output), then it's called a quadratic function Usually, you would give that function a name f(x) = ax 2 bx c
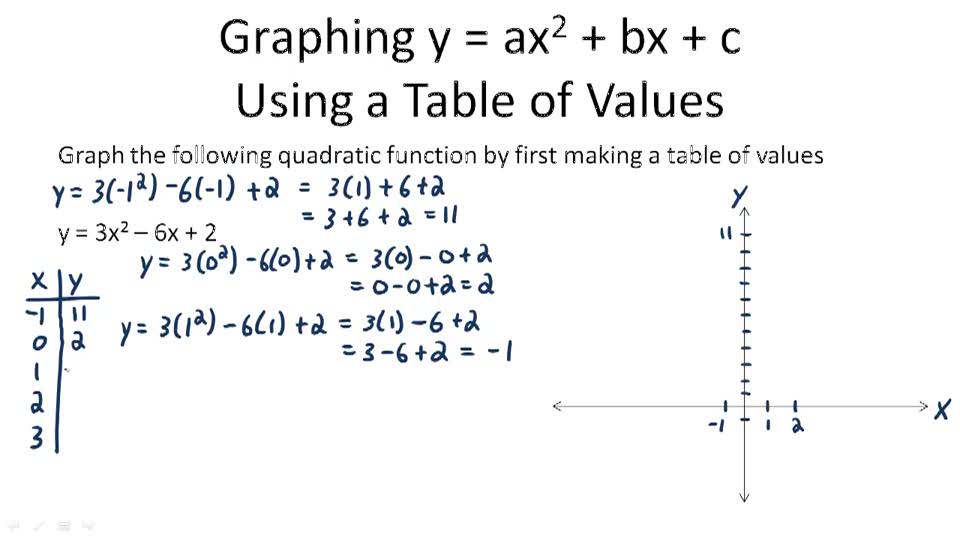



Graphing Quadratic Functions Of The Form Y Ax 2 Bx C Example 1 Video Algebra Ck 12 Foundation
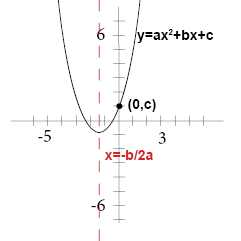



How Do You Graph F X 3x 2 4x 1 Socratic
$$ax^2bxc=(AxB)(dxe)C \ \ \text{for certain real numbers} \ \ A,B,C$$ Thus $$f(x)=y=AxB\dfrac{C}{dxe} \ \ \text{with} \ \ A=\frac{a}{d} \neq 0 \ \ (1)$$ Two cases Either $C=0$ (which happens when $dxe$ exactly divides $ax^2bxc$) in this case, the graphical representation of $f$ is a straight line which is its own symmetry axis and has an infinite number7 Starting with from both sides Add the square of onehalf of b/a, the coefficient of x, to both sides This "completes the square", converting the left side into a perfect squareWe now present examples and details of several of the preset models available 1 Linear Y=ABX 23 Power^Power Y=AX^(BX^C) 24 Sum of Exponentials Y=A(EXP(BX))C(EXP(DX)) 25 Exponential Type 1 Y=A(X^B)EXP( CX) 26 Exponential Type 2 Y=(ABX)EXP( CX)D Plot of Y = X^X X Y Plot of Y = X^(X) X Y




Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange



Unique Quadratic Equation In The Form Y Ax 2 Bx C
Standard Form y = ax2 bx c Vertex Form y = a(x – h)2 k Convert from Standard Form to Vertex Form y = ax 2 bx = c y = a(x – h) k know a, b, c want a, h, k a = a = h Solve for y = k Substitute the values and rewrite Example 1 y = 8x2 – 16x 27 We know a, b, c and want a, h, k a = 8 a is the coefficient of the x 2 term hBy examining "a" in f (x)= ax2 bx c, it can be determined whether the function has a maximum value (opens up) or a minimum value (opens down) Example #2 Determine if vertex of the quadratic function is a minimum or a maximum point in its parabola and if the parabola opens upward or downward a) f (x)= –5x 2x2 2 b) g (x)= 7 – 6x – 2x2R How to solve an equation y=ax^2bxc when x is unknown and y known Stack Overflow I have this equation y = *x^*x And I would like to obtain the result of the equation when I give "y" numbers,



1




Quadratic Graph Example Y Ax C Expii
Learn how to graph a parabola of the form f(x)=ax^2bxc with integer coefficients, and see examples that walk through sample problems stepbystep for you to improve your math knowledge and skillsAlgebra Examples Popular Problems Algebra Solve for x y=ax^2bxc Rewrite the equation as Move to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values , , and into the quadratic formula and solve forStep 2 calculate the \(y\)coordinate of the vertex, \(k\), by replacing \(x\) inside \(y=ax^2bxc\) and calculating the value of \(y\) Tutorial Coordinates of the Vertex In the following tutorial we learn how to find the coordinates of a parabola's vertex , in other words the coordinates of its maximum, or minimum, point
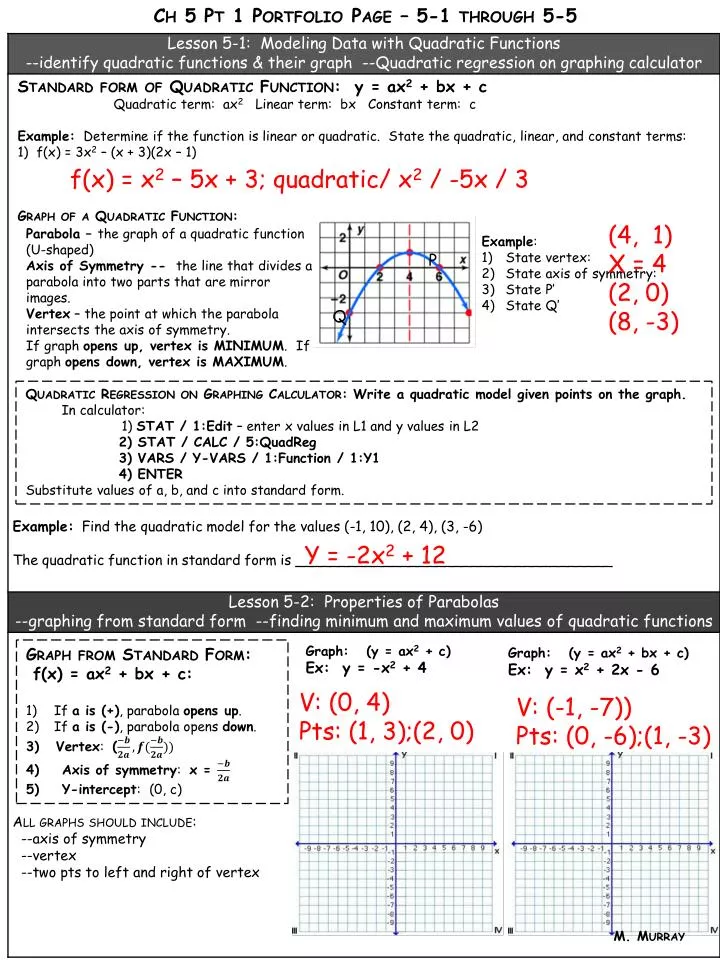



Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id



1
Problem 70 Hard Difficulty Find a parabola with equation $ y = ax^2 bx c $ that has slope 4 at $ x = 1, $ slope 8 at $ x = 1, $ and passes through the point (2, 15)Exploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




Factoring Trinomials Of The Form Ax 2 Bx C



Program To Find The Roots Of Quadratic Equation Geeksforgeeks




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download
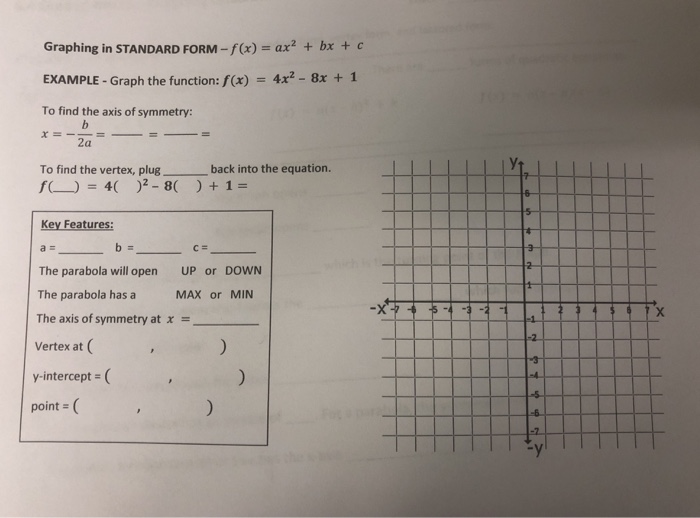



Graphing In Standard Form F X Ax2 Bx C Chegg Com



Quadratics
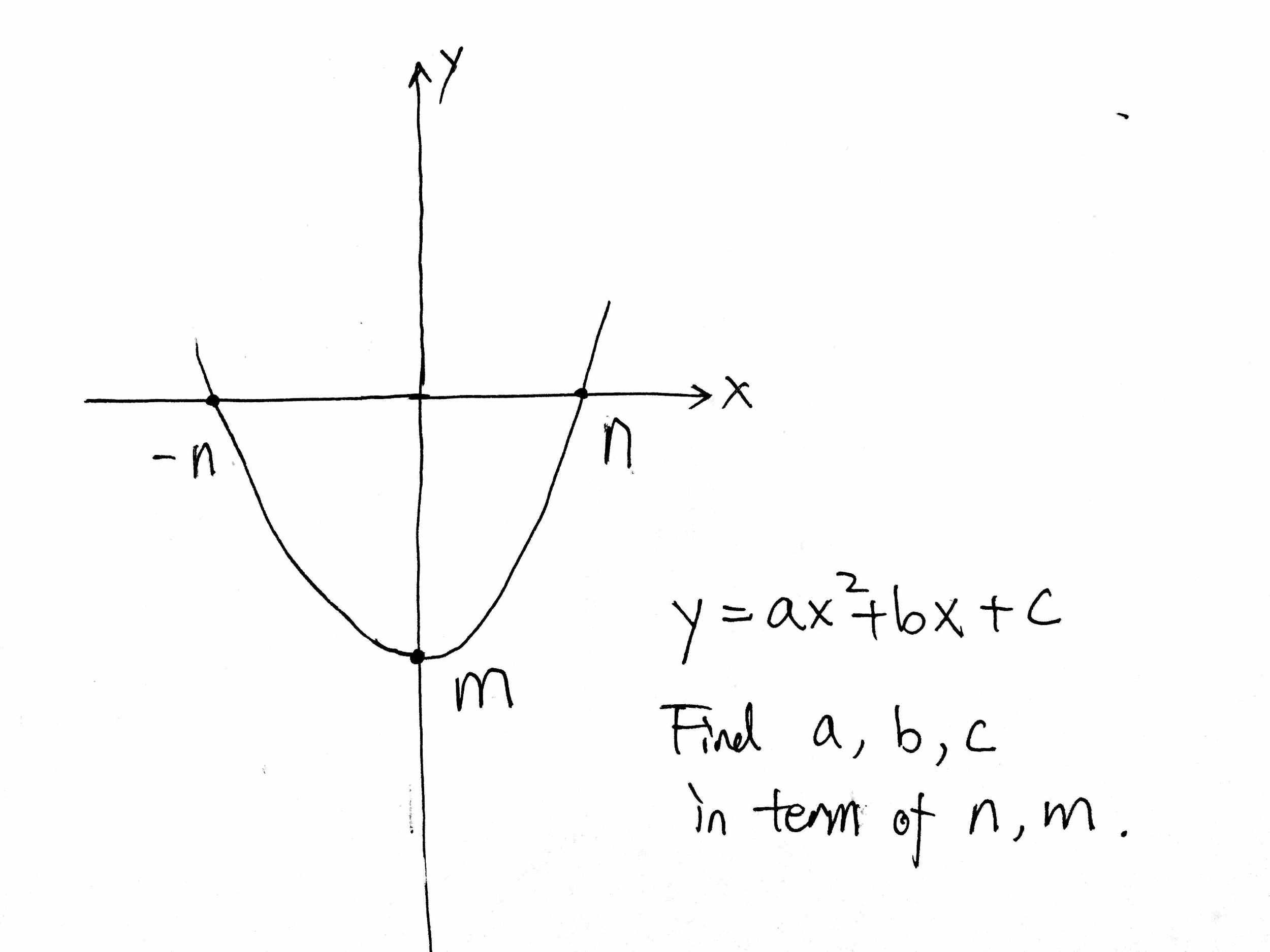



Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com




Quadratic Graph Example Y Ax Expii
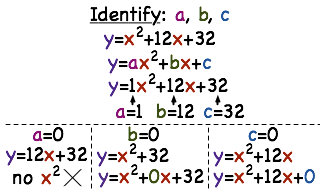



How Do You Find The A B And C Values Of A Quadratic Function Printable Summary Virtual Nerd
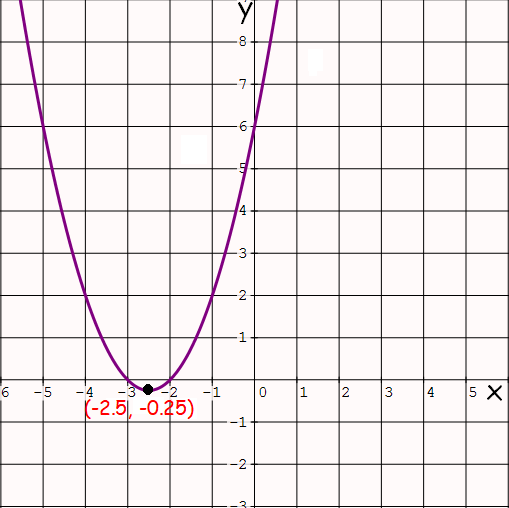



Domain And Range Of A Quadratic Function



Quadratics



Unique Quadratic Equation In The Form Y Ax 2 Bx C



Exploring Parabolas Y Ax 2 Bx C




The Given Figure Shows The Graph Of The Polynomial F X Ax 2 Bx C Then Ltbr Gt 1 Nbsp Youtube




Trinomials Of The Form Ax 2 Bx C




Use The Standard Form Of A Parabola Given By Y Ax2 Bx Chegg Com



Unique Quadratic Equation In The Form Y Ax 2 Bx C



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora



Unique Quadratic Equation In The Form Y Ax 2 Bx C
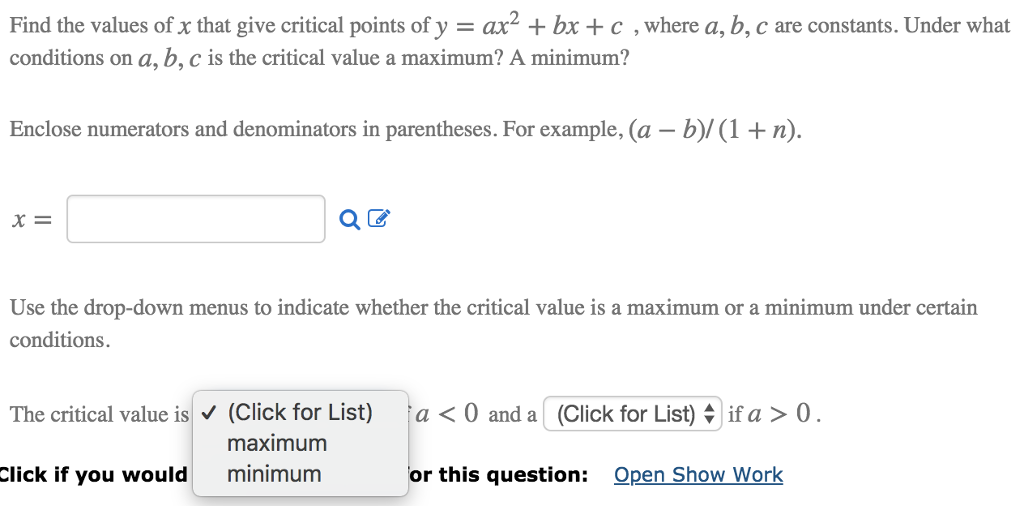



Find The Values Of X That Give Critical Points Of Y Chegg Com




Graphing Y Ax 2 Bx C



For All Functions Of The Form F X Ax2 Bx C Which Is True When B 0 Quora




Graph Of Quadratic Expression Y Ax 2 Bx C Is Given Then




Quadratic Equation Wikipedia




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi
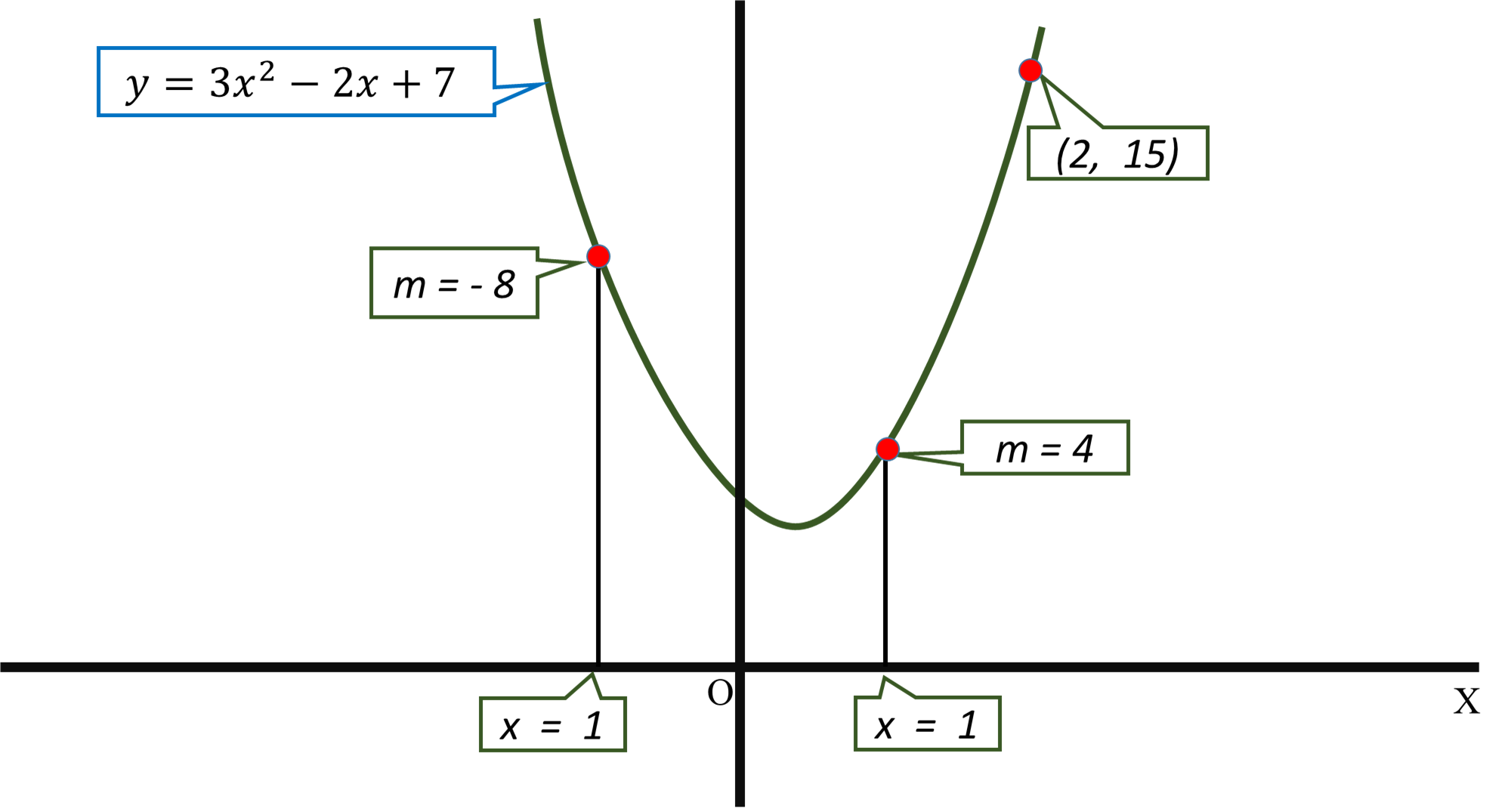



How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic



Math Spoken Here About Quadratics 3




The Adjoining Figure Shows The Graph Of Y Ax 2 Bx C Then Youtube




Exploring Quadratic Graphs Ppt Video Online Download



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id
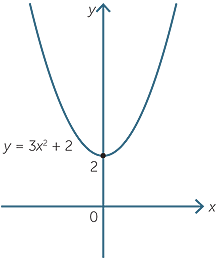



Quadratic Function




Ppt Vertex Form Powerpoint Presentation Free Download Id




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube
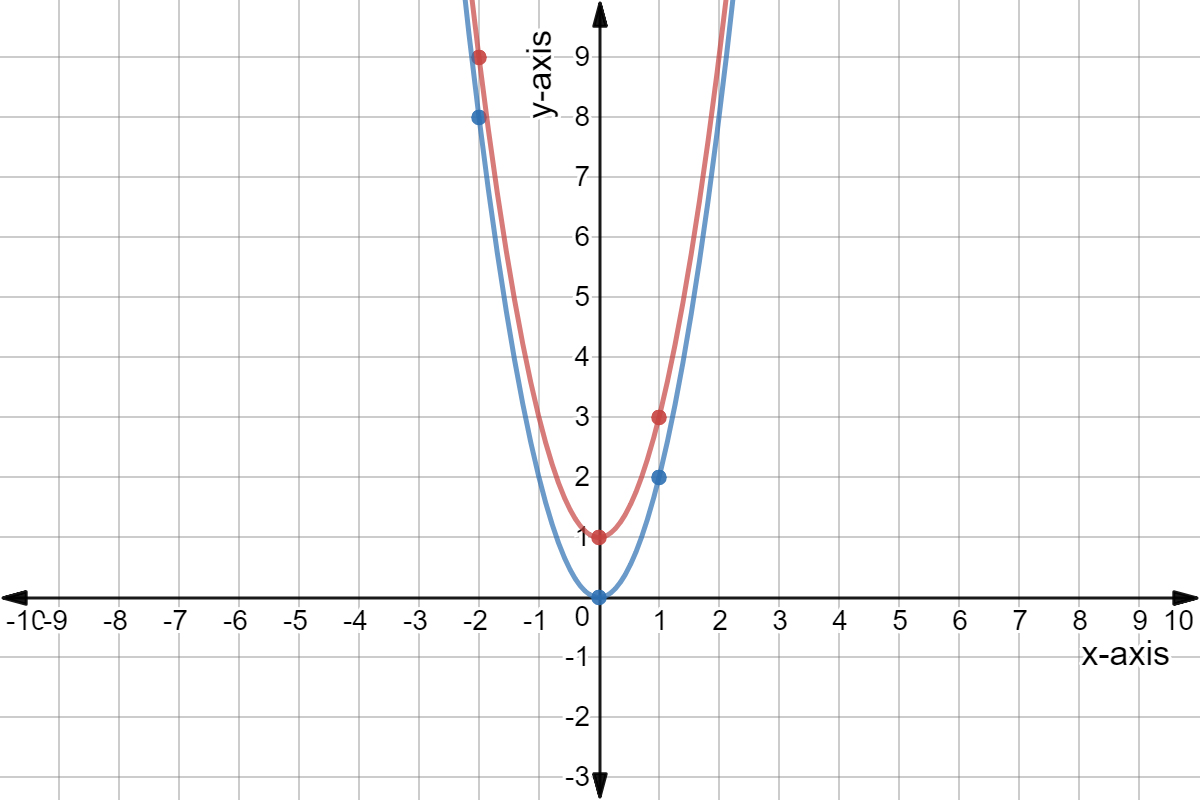



Quadratic Graph Example Y Ax C Expii



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
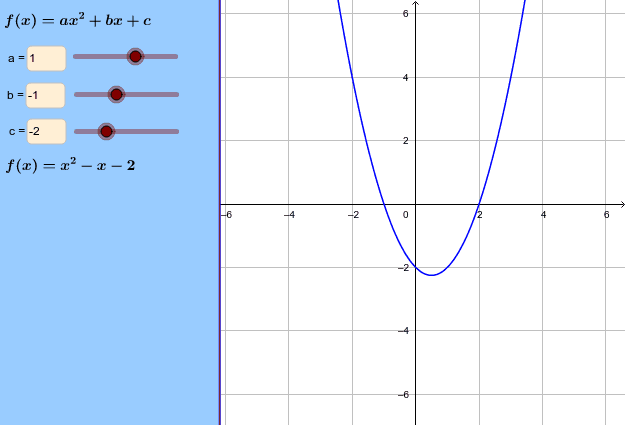



The Graph Of Y Ax 2 Bx C Geogebra



1




The Expression Y Ax 2 Bx C Has Always The Same Sign As Of A If A 4ac Lt B 2 B 4ac Youtube



What Is The Difference Between Ax 2 Bx C And X 2 Bx C In A Quadratic Equation Perspective Quora




Use The Graph Of Y Ax2 Bx C To Solve A Chegg Com




8 3 Graphing F X Ax 2 Bx C Youtube
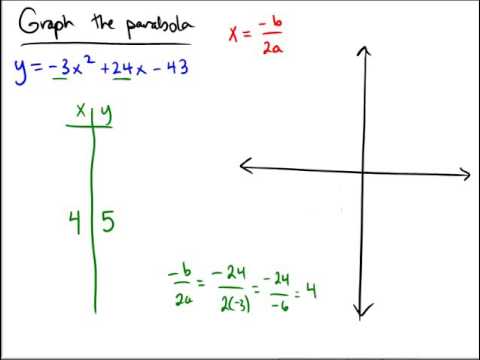



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube



Quadratic Function Wikipedia




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download



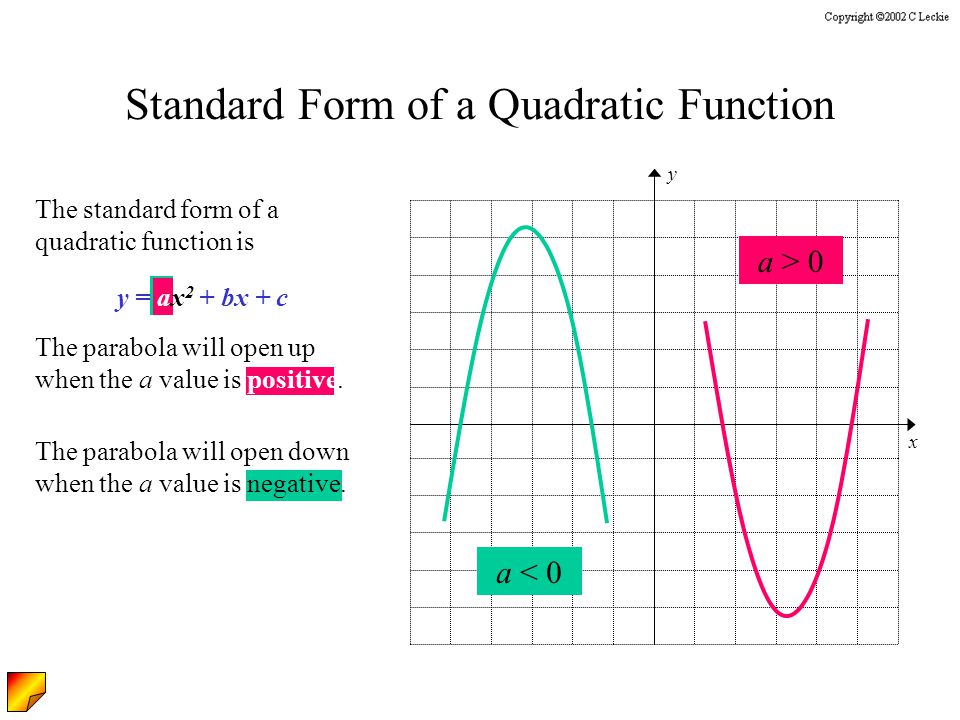
Quadratic Function Wikipedia



Unique Quadratic Equation In The Form Y Ax 2 Bx C



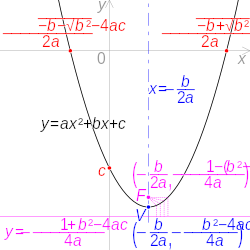
Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download



Examining The Parabola Assignment 2




Factoring Trinomials Of The Form Ax 2 Bx C




Finding The Inverse Of Y Ax2 Bx C By Completing The Square Youtube



How Does The Middle Term Of A Quadratic Ax 2 Bx C Influence The Graph Of Y X 2 Mathematics Stack Exchange




Y Ax2 Bx C Quadratic Function Ppt Download



What Is The X Coordinate Of The Vertex Of Parabola Whose Equation Is Y Ax2 Bx C 0 A 0 Quora
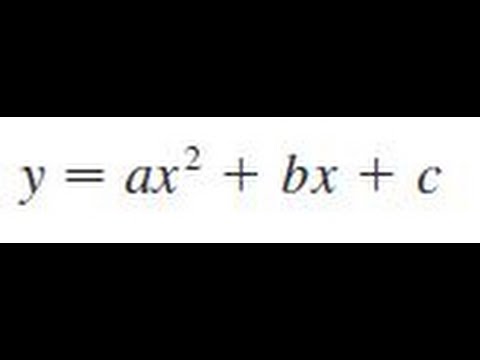



Differentiate The Function Y Ax 2 Bx C Youtube



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




How Do You Find A Quadratic Function F X Ax 2 Bx C For Which F 1 2 F 3 46 And F 3 16 Socratic
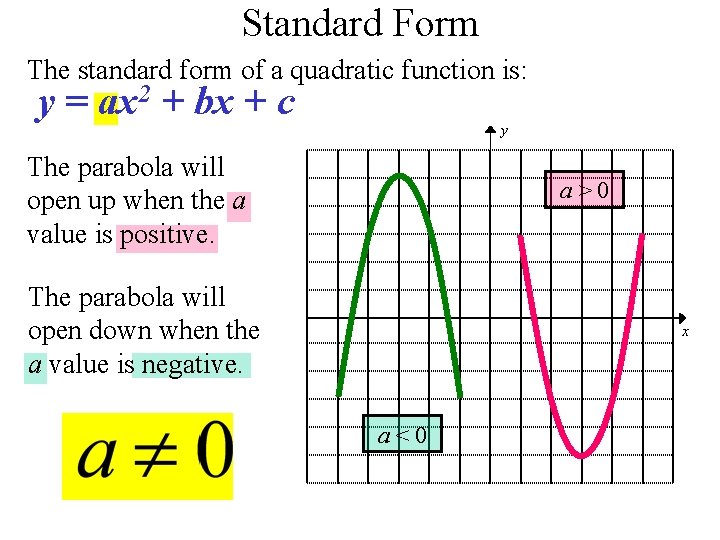



Graphing Quadratic Functions Ma 912 A 7 1




Consider The Graph Of F X Ax 2 Bx C In The Adjacent Figure We Can Conclude That




Graphing Y Ax 2 Bx C




Graphing Quadratic Functions Y Ax 2 Bx C



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




यद Y Ax 2 Bx C त Dy Dx न क ल




Review Y Ax2 Bx C Is A Parabola If A 0 The Parabola Is Oriented Upward And The Vertex Is The Minimum Point Of The Function If A 0 The Ppt Download




Factoring Ax2 Bx C Worksheet Answers Worksheet List
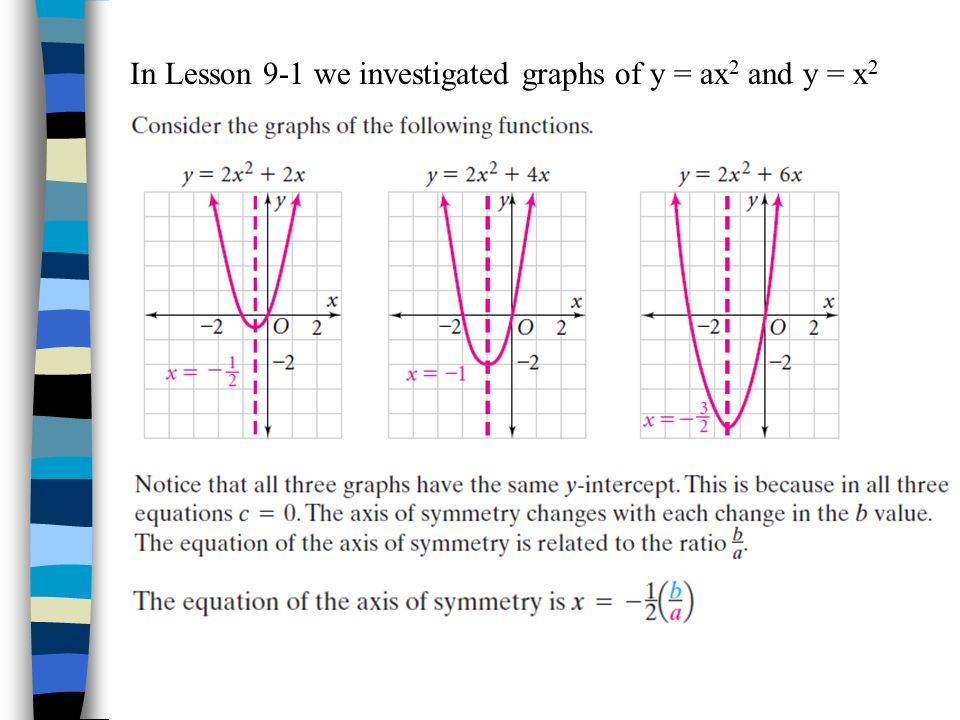



Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download




If Graph Of Y Ax 2 Bx C Is As Shown Then Which Of The Following Is Correct Where D Equals B 2 4ac
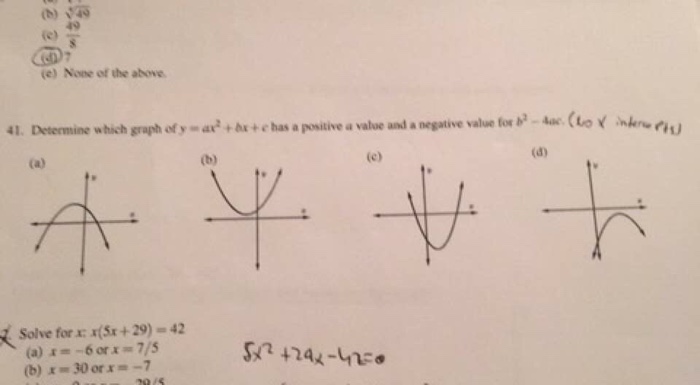



Determine Which Graph Of Y Ax 2 Bx C Has A Chegg Com
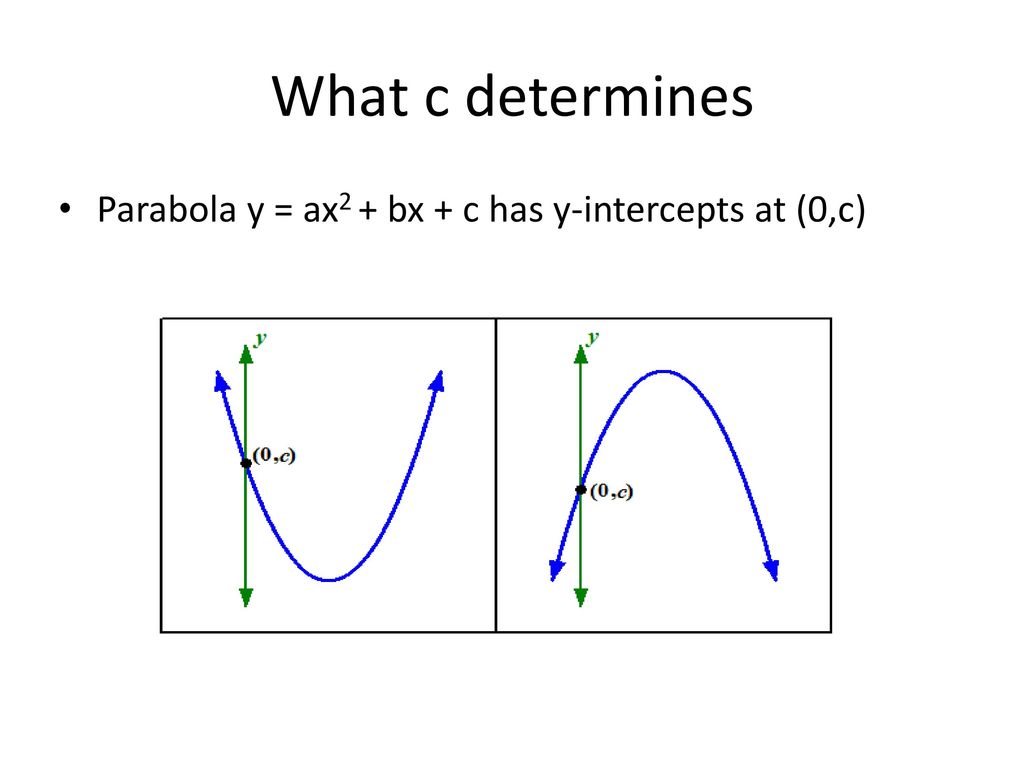



How To Draw A Parabola Ppt Download




Graphing Y Ax2 Bx C Youtube



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Standard Form Y Ax2 Bx C Factored Form Y A X S X T




The Equation Of A Parabola Is Y Ax 2 Bx C Use A For Chegg Com



What Is The Difference Between Ax 2 Bx C And X 2 Bx C In A Quadratic Equation Perspective Quora




B Value Definition Explanation Video Lesson Transcript Study Com




View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A



Www Cgsd Org Site Handlers Filedownload Ashx Moduleinstanceid 280 Dataid 1438 Filename 393 Smp Seaa C06l04 Pdf



Sometimesmath Weebly Com Uploads 1 1 8 3 1129 Graphing Ax 5e2 Bx C Pdf
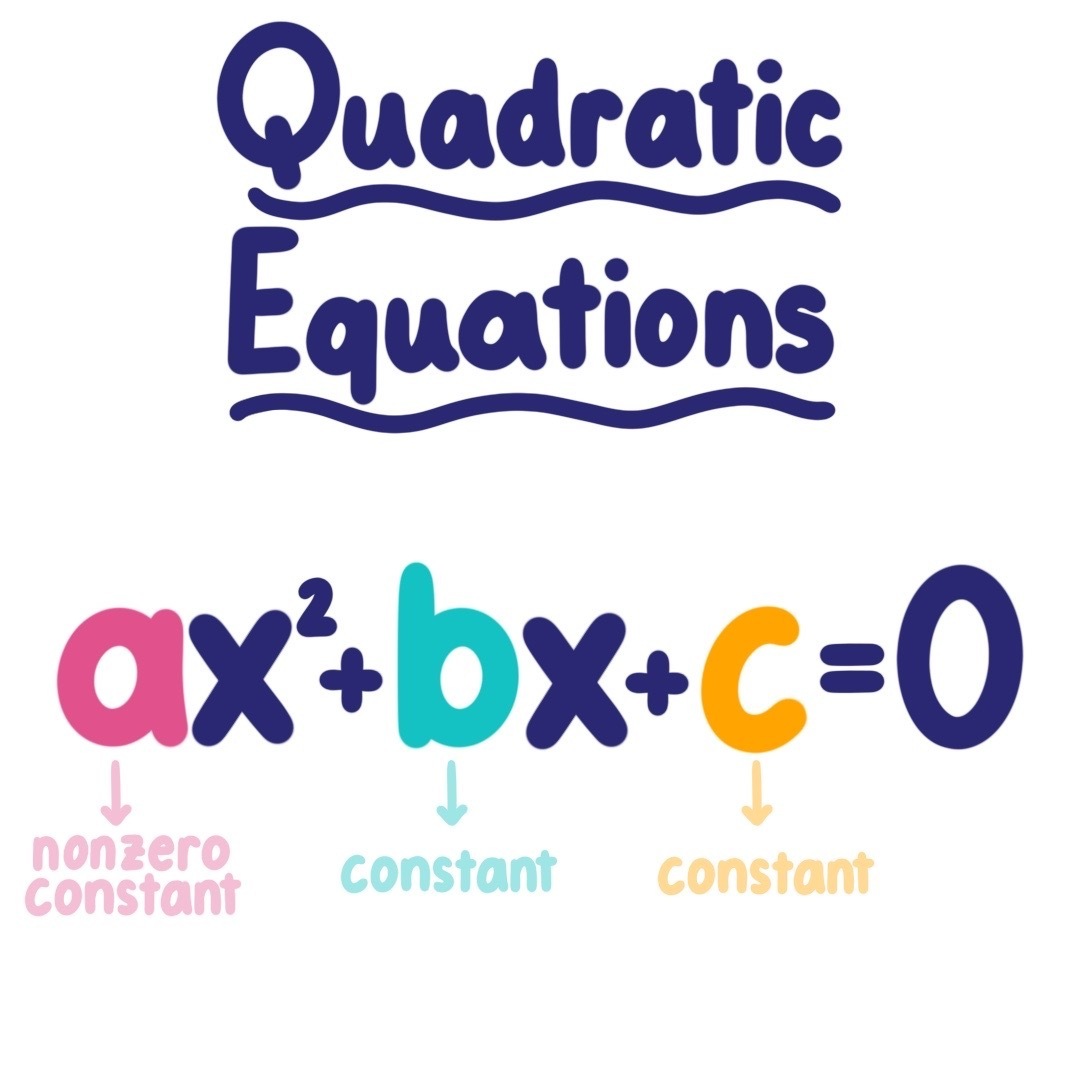



Quadratic Equations Definition Examples Expii



0 件のコメント:
コメントを投稿